题目
(3)曲线 =(x)^2 与曲线 =aln x(aneq 0) 相切,则a等于 ()-|||-(A)4e (B) 3e (C) 2e (D) e

题目解答
答案
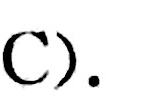
解析
步骤 1:确定切点
设曲线 $y=x^2$ 与曲线 $y=a\ln x$ 在点 $(x_0, y_0)$ 处相切,则有 $y_0 = x_0^2$ 和 $y_0 = a\ln x_0$。因此,$x_0^2 = a\ln x_0$。
步骤 2:确定切线斜率
曲线 $y=x^2$ 在点 $(x_0, y_0)$ 处的斜率为 $y' = 2x_0$。曲线 $y=a\ln x$ 在点 $(x_0, y_0)$ 处的斜率为 $y' = \frac{a}{x_0}$。由于两曲线在该点相切,斜率相等,即 $2x_0 = \frac{a}{x_0}$。
步骤 3:求解 $a$
由 $2x_0 = \frac{a}{x_0}$,得 $a = 2x_0^2$。将 $a = 2x_0^2$ 代入 $x_0^2 = a\ln x_0$,得 $x_0^2 = 2x_0^2\ln x_0$。化简得 $\ln x_0 = \frac{1}{2}$,从而 $x_0 = e^{\frac{1}{2}} = \sqrt{e}$。因此,$a = 2x_0^2 = 2(\sqrt{e})^2 = 2e$。
设曲线 $y=x^2$ 与曲线 $y=a\ln x$ 在点 $(x_0, y_0)$ 处相切,则有 $y_0 = x_0^2$ 和 $y_0 = a\ln x_0$。因此,$x_0^2 = a\ln x_0$。
步骤 2:确定切线斜率
曲线 $y=x^2$ 在点 $(x_0, y_0)$ 处的斜率为 $y' = 2x_0$。曲线 $y=a\ln x$ 在点 $(x_0, y_0)$ 处的斜率为 $y' = \frac{a}{x_0}$。由于两曲线在该点相切,斜率相等,即 $2x_0 = \frac{a}{x_0}$。
步骤 3:求解 $a$
由 $2x_0 = \frac{a}{x_0}$,得 $a = 2x_0^2$。将 $a = 2x_0^2$ 代入 $x_0^2 = a\ln x_0$,得 $x_0^2 = 2x_0^2\ln x_0$。化简得 $\ln x_0 = \frac{1}{2}$,从而 $x_0 = e^{\frac{1}{2}} = \sqrt{e}$。因此,$a = 2x_0^2 = 2(\sqrt{e})^2 = 2e$。