题目
lim _(xarrow 0)((cos x))^dfrac (1{ln (1+{x)^2)}}.
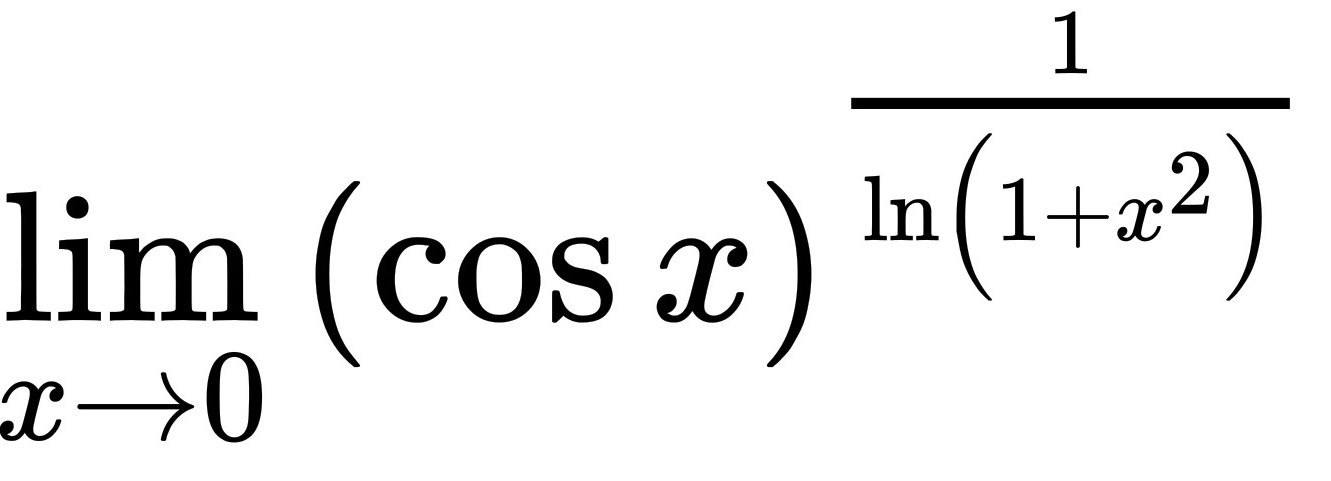 .
.
题目解答
答案
原式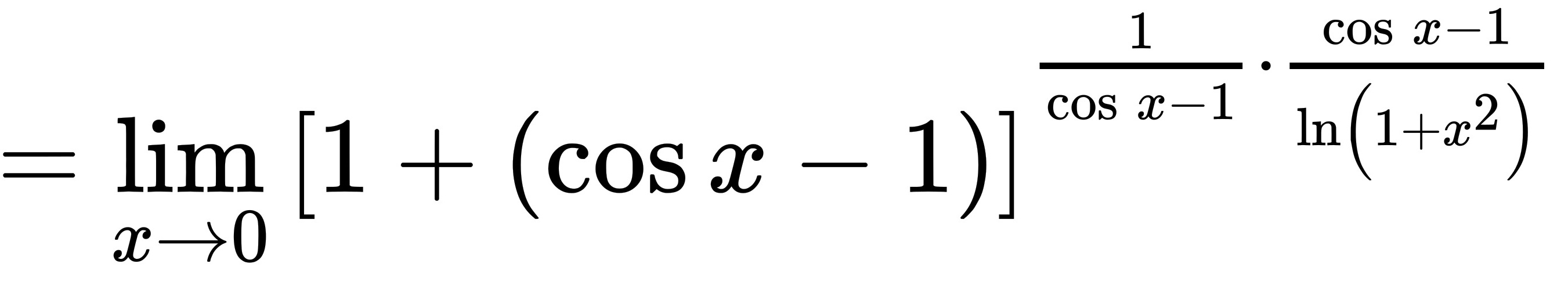
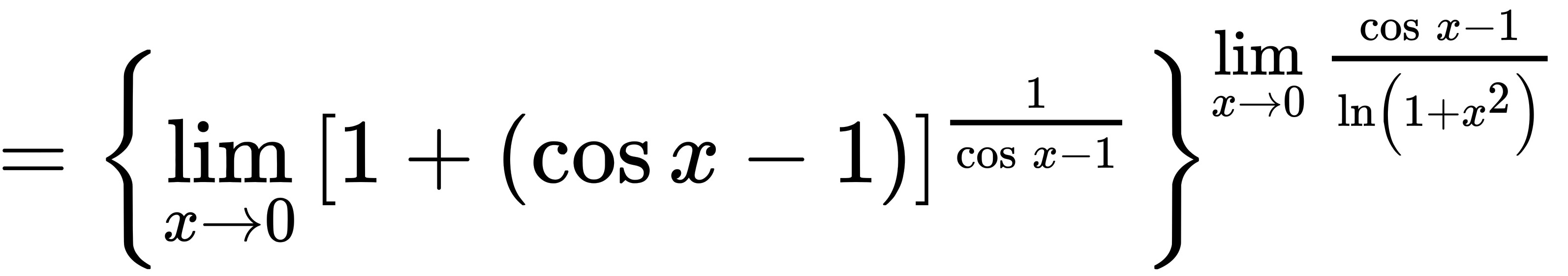
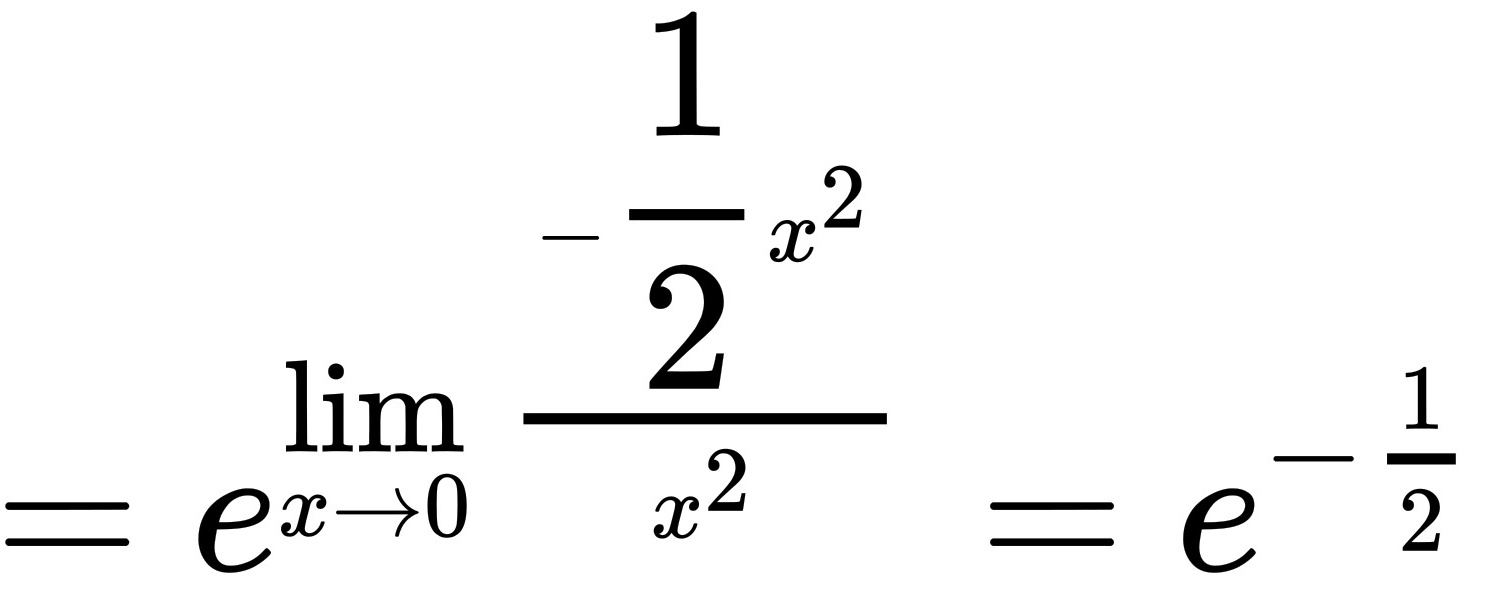
解析
步骤 1:将原式转换为指数形式
原式可以写成 $e^{\ln((\cos x)^{\ln(1+x^2)})}$,即 $e^{\ln(1+x^2) \cdot \ln(\cos x)}$。
步骤 2:利用等价无穷小替换
当 $x \rightarrow 0$ 时,$\ln(1+x^2) \sim x^2$,$\ln(\cos x) \sim -\frac{x^2}{2}$。
步骤 3:代入等价无穷小并计算极限
将等价无穷小代入原式,得到 $e^{x^2 \cdot (-\frac{x^2}{2})} = e^{-\frac{x^4}{2}}$。
步骤 4:计算极限
当 $x \rightarrow 0$ 时,$e^{-\frac{x^4}{2}} \rightarrow e^0 = 1$。
原式可以写成 $e^{\ln((\cos x)^{\ln(1+x^2)})}$,即 $e^{\ln(1+x^2) \cdot \ln(\cos x)}$。
步骤 2:利用等价无穷小替换
当 $x \rightarrow 0$ 时,$\ln(1+x^2) \sim x^2$,$\ln(\cos x) \sim -\frac{x^2}{2}$。
步骤 3:代入等价无穷小并计算极限
将等价无穷小代入原式,得到 $e^{x^2 \cdot (-\frac{x^2}{2})} = e^{-\frac{x^4}{2}}$。
步骤 4:计算极限
当 $x \rightarrow 0$ 时,$e^{-\frac{x^4}{2}} \rightarrow e^0 = 1$。