题目
1 求下列函数的导数 =((x+sqrt {{x)^2+1})}^n
1 求下列函数的导数
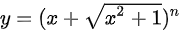
题目解答
答案
解:
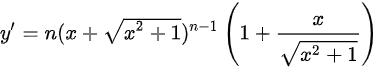
解析
步骤 1:应用链式法则
链式法则用于求复合函数的导数。给定函数 $y={(x+\sqrt {{x}^{2}+1})}^{n}$,我们首先识别外层函数为 $u^n$,其中 $u=x+\sqrt {{x}^{2}+1}$,内层函数为 $u=x+\sqrt {{x}^{2}+1}$。根据链式法则,$y'$ 可以表示为 $n{(x+\sqrt {{x}^{2}+1})}^{n-1}$ 乘以内层函数 $u$ 的导数。
步骤 2:求内层函数的导数
内层函数 $u=x+\sqrt {{x}^{2}+1}$ 的导数需要分别对 $x$ 和 $\sqrt {{x}^{2}+1}$ 求导。$x$ 的导数为 $1$,而 $\sqrt {{x}^{2}+1}$ 的导数为 $\dfrac {x}{\sqrt {{x}^{2}+1}}$,因为 $\sqrt {{x}^{2}+1}$ 可以看作是 $(x^2+1)^{1/2}$,其导数为 $\dfrac {1}{2}(x^2+1)^{-1/2} \cdot 2x = \dfrac {x}{\sqrt {{x}^{2}+1}}$。
步骤 3:组合结果
将步骤 1 和步骤 2 的结果组合起来,得到 $y'$ 的表达式。即 $y'=n{(x+\sqrt {{x}^{2}+1})}^{n-1} \cdot (1+\dfrac {x}{\sqrt {{x}^{2}+1}})$。
链式法则用于求复合函数的导数。给定函数 $y={(x+\sqrt {{x}^{2}+1})}^{n}$,我们首先识别外层函数为 $u^n$,其中 $u=x+\sqrt {{x}^{2}+1}$,内层函数为 $u=x+\sqrt {{x}^{2}+1}$。根据链式法则,$y'$ 可以表示为 $n{(x+\sqrt {{x}^{2}+1})}^{n-1}$ 乘以内层函数 $u$ 的导数。
步骤 2:求内层函数的导数
内层函数 $u=x+\sqrt {{x}^{2}+1}$ 的导数需要分别对 $x$ 和 $\sqrt {{x}^{2}+1}$ 求导。$x$ 的导数为 $1$,而 $\sqrt {{x}^{2}+1}$ 的导数为 $\dfrac {x}{\sqrt {{x}^{2}+1}}$,因为 $\sqrt {{x}^{2}+1}$ 可以看作是 $(x^2+1)^{1/2}$,其导数为 $\dfrac {1}{2}(x^2+1)^{-1/2} \cdot 2x = \dfrac {x}{\sqrt {{x}^{2}+1}}$。
步骤 3:组合结果
将步骤 1 和步骤 2 的结果组合起来,得到 $y'$ 的表达式。即 $y'=n{(x+\sqrt {{x}^{2}+1})}^{n-1} \cdot (1+\dfrac {x}{\sqrt {{x}^{2}+1}})$。