题目
2.求极限 lim _(xarrow +infty )arcsin dfrac (x)(sqrt {{x)^2+1}+x}

题目解答
答案
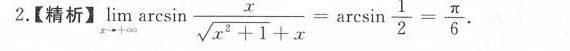
解析
步骤 1:化简极限中的表达式
首先,我们观察到极限中的表达式 $\dfrac {x}{\sqrt {{x}^{2}+1}+x}$,当 $x$ 趋于正无穷时,分母中的 $\sqrt{x^2+1}$ 项和 $x$ 项都趋于无穷大。为了简化这个表达式,我们可以将分子和分母同时除以 $x$,这样可以将表达式中的 $x$ 因子消去,从而更容易分析极限。
步骤 2:计算简化后的极限
将分子和分母同时除以 $x$,得到 $\dfrac {1}{\sqrt {1+\frac{1}{x^2}}+1}$。当 $x$ 趋于正无穷时,$\frac{1}{x^2}$ 趋于 0,因此 $\sqrt {1+\frac{1}{x^2}}$ 趋于 $\sqrt{1}$,即 1。所以,原表达式趋于 $\dfrac {1}{1+1} = \dfrac {1}{2}$。
步骤 3:计算最终的极限值
由于 $\arcsin$ 函数是连续的,我们可以将极限值代入 $\arcsin$ 函数中,得到 $\arcsin \dfrac {1}{2}$。根据 $\arcsin$ 函数的定义,$\arcsin \dfrac {1}{2} = \dfrac {\pi }{6}$。
首先,我们观察到极限中的表达式 $\dfrac {x}{\sqrt {{x}^{2}+1}+x}$,当 $x$ 趋于正无穷时,分母中的 $\sqrt{x^2+1}$ 项和 $x$ 项都趋于无穷大。为了简化这个表达式,我们可以将分子和分母同时除以 $x$,这样可以将表达式中的 $x$ 因子消去,从而更容易分析极限。
步骤 2:计算简化后的极限
将分子和分母同时除以 $x$,得到 $\dfrac {1}{\sqrt {1+\frac{1}{x^2}}+1}$。当 $x$ 趋于正无穷时,$\frac{1}{x^2}$ 趋于 0,因此 $\sqrt {1+\frac{1}{x^2}}$ 趋于 $\sqrt{1}$,即 1。所以,原表达式趋于 $\dfrac {1}{1+1} = \dfrac {1}{2}$。
步骤 3:计算最终的极限值
由于 $\arcsin$ 函数是连续的,我们可以将极限值代入 $\arcsin$ 函数中,得到 $\arcsin \dfrac {1}{2}$。根据 $\arcsin$ 函数的定义,$\arcsin \dfrac {1}{2} = \dfrac {\pi }{6}$。