题目
yy-|||-0 C x-|||-B-|||-H已知抛物线y=x2+2x+c与x轴负半轴、y轴的负半轴分别交于点A、B,与x轴正半轴交于点C,且满足OA=OB.(1)求抛物线的解析式及顶点H的坐标;(2)过y轴上一动点Q(0,q)作平行于x轴的水平直线交抛物线于E,F两点,若线段EF长为5,求q的值;(3)已知点P(-3,1),Q(2,2t+1),且线段PQ与抛物线y=x2+2x+c有且只有一个公共点,直接写出t的取值范围.
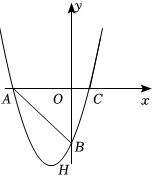 已知抛物线y=x2+2x+c与x轴负半轴、y轴的负半轴分别交于点A、B,与x轴正半轴交于点C,且满足OA=OB.
已知抛物线y=x2+2x+c与x轴负半轴、y轴的负半轴分别交于点A、B,与x轴正半轴交于点C,且满足OA=OB.(1)求抛物线的解析式及顶点H的坐标;
(2)过y轴上一动点Q(0,q)作平行于x轴的水平直线交抛物线于E,F两点,若线段EF长为5,求q的值;
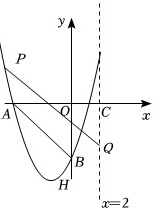
(3)已知点P(-3,1),Q(2,2t+1),且线段PQ与抛物线y=x2+2x+c有且只有一个公共点,直接写出t的取值范围.
题目解答
答案
解:(1)y=x2+2x+c与x轴负半轴、y轴的负半轴分别交于点A、B,
当x=0时,y=c,
∴c<0,B(0,c),
∵OA=OB,
∴A(c,0),
∴0=c2+2c+c,解得:c=-3或c=0(不合题意,舍去),
∴抛物线的解析式为:y=x2+2x-3;
∵y=x2+2x-3=(x+1)2-4,
∴抛物线的顶点坐标:H(-1,-4);
(2)∵EF∥x轴,
∴点E,Q,F三点的纵坐标相同,均为q,
∴点E,F关于对称轴对称,
由(1)可知:抛物线的对称轴为直线x=-1,
∵EF=5,
∴E,F两点的横坐标分别为:$-1+\frac{5}{2}=\frac{3}{2},-1-\frac{5}{2}=-\frac{7}{2}$,
当$x=\frac{3}{2}$时,$y={({\frac{3}{2}})^2}+2×\frac{3}{2}-3=\frac{9}{4}$,即:$q=\frac{9}{4}$;
(3)由(1)可知:A(-3,0),
∴点P(-3,1)不在抛物线上,
∵Q(2,2t+1),
∴点Q在直线x=2上,
∵y=x2+2x-3,
当x=2时,y=22+2×2-3=5,
∴当2t+1≤5时,即:t≤2时,线段与线段PQ与抛物线y=x2+2x+c有且只有一个公共点.
当x=0时,y=c,
∴c<0,B(0,c),
∵OA=OB,
∴A(c,0),
∴0=c2+2c+c,解得:c=-3或c=0(不合题意,舍去),
∴抛物线的解析式为:y=x2+2x-3;
∵y=x2+2x-3=(x+1)2-4,
∴抛物线的顶点坐标:H(-1,-4);
(2)∵EF∥x轴,
∴点E,Q,F三点的纵坐标相同,均为q,
∴点E,F关于对称轴对称,
由(1)可知:抛物线的对称轴为直线x=-1,
∵EF=5,
∴E,F两点的横坐标分别为:$-1+\frac{5}{2}=\frac{3}{2},-1-\frac{5}{2}=-\frac{7}{2}$,
当$x=\frac{3}{2}$时,$y={({\frac{3}{2}})^2}+2×\frac{3}{2}-3=\frac{9}{4}$,即:$q=\frac{9}{4}$;
(3)由(1)可知:A(-3,0),
∴点P(-3,1)不在抛物线上,
∵Q(2,2t+1),
∴点Q在直线x=2上,
∵y=x2+2x-3,
当x=2时,y=22+2×2-3=5,
∴当2t+1≤5时,即:t≤2时,线段与线段PQ与抛物线y=x2+2x+c有且只有一个公共点.

解析
步骤 1:确定抛物线的解析式
抛物线与x轴负半轴、y轴的负半轴分别交于点A、B,与x轴正半轴交于点C,且满足OA=OB。当x=0时,y=c,所以B(0,c),且c<0。因为OA=OB,所以A(c,0)。将A点坐标代入抛物线方程,得到0=c^2+2c+c,解得c=-3或c=0(不合题意,舍去)。因此,抛物线的解析式为y=x^2+2x-3。
步骤 2:求顶点H的坐标
抛物线的解析式为y=x^2+2x-3,将其化为顶点式y=(x+1)^2-4,所以顶点H的坐标为(-1,-4)。
步骤 3:求q的值
过y轴上一动点Q(0,q)作平行于x轴的水平直线交抛物线于E,F两点,若线段EF长为5。因为EF∥x轴,所以点E,Q,F三点的纵坐标相同,均为q。点E,F关于对称轴对称,由(1)可知:抛物线的对称轴为直线x=-1。因为EF=5,所以E,F两点的横坐标分别为:$-1+\frac{5}{2}=\frac{3}{2},-1-\frac{5}{2}=-\frac{7}{2}$。当$x=\frac{3}{2}$时,$y={({\frac{3}{2}})^2}+2×\frac{3}{2}-3=\frac{9}{4}$,即:$q=\frac{9}{4}$。
步骤 4:求t的取值范围
由(1)可知:A(-3,0),所以点P(-3,1)不在抛物线上。因为Q(2,2t+1),所以点Q在直线x=2上。因为y=x^2+2x-3,当x=2时,y=2^2+2×2-3=5,所以当2t+1≤5时,即:t≤2时,线段与线段PQ与抛物线y=x^2+2x+c有且只有一个公共点。
抛物线与x轴负半轴、y轴的负半轴分别交于点A、B,与x轴正半轴交于点C,且满足OA=OB。当x=0时,y=c,所以B(0,c),且c<0。因为OA=OB,所以A(c,0)。将A点坐标代入抛物线方程,得到0=c^2+2c+c,解得c=-3或c=0(不合题意,舍去)。因此,抛物线的解析式为y=x^2+2x-3。
步骤 2:求顶点H的坐标
抛物线的解析式为y=x^2+2x-3,将其化为顶点式y=(x+1)^2-4,所以顶点H的坐标为(-1,-4)。
步骤 3:求q的值
过y轴上一动点Q(0,q)作平行于x轴的水平直线交抛物线于E,F两点,若线段EF长为5。因为EF∥x轴,所以点E,Q,F三点的纵坐标相同,均为q。点E,F关于对称轴对称,由(1)可知:抛物线的对称轴为直线x=-1。因为EF=5,所以E,F两点的横坐标分别为:$-1+\frac{5}{2}=\frac{3}{2},-1-\frac{5}{2}=-\frac{7}{2}$。当$x=\frac{3}{2}$时,$y={({\frac{3}{2}})^2}+2×\frac{3}{2}-3=\frac{9}{4}$,即:$q=\frac{9}{4}$。
步骤 4:求t的取值范围
由(1)可知:A(-3,0),所以点P(-3,1)不在抛物线上。因为Q(2,2t+1),所以点Q在直线x=2上。因为y=x^2+2x-3,当x=2时,y=2^2+2×2-3=5,所以当2t+1≤5时,即:t≤2时,线段与线段PQ与抛物线y=x^2+2x+c有且只有一个公共点。