题目
求极限lim _(xarrow 0)dfrac (1)({x)^3}[ ((dfrac {2+cos x)(3))}^x-1] -|||-__
求极限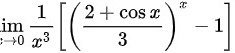
题目解答
答案
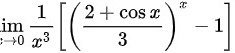
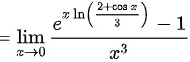
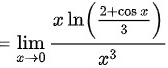
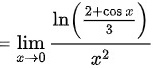
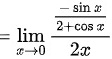
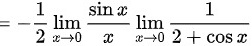
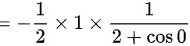
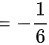
故答案为: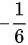
解析
步骤 1:化简极限表达式
首先,我们注意到极限表达式中包含指数函数和多项式。为了简化问题,我们使用对数的性质,将指数函数转化为对数形式。具体地,我们有:
$$\lim _{x\rightarrow 0}\dfrac {1}{{x}^{3}}[ {(\dfrac {2+\cos x}{3})}^{x}-1] = \lim _{x\rightarrow 0}\dfrac {1}{{x}^{3}}[e^{x\ln(\frac{2+\cos x}{3})}-1]$$
步骤 2:利用泰勒展开
接下来,我们利用$e^y$的泰勒展开式,其中$y=x\ln(\frac{2+\cos x}{3})$。泰勒展开式为:
$$e^y = 1 + y + \frac{y^2}{2!} + \frac{y^3}{3!} + \cdots$$
因此,我们有:
$$e^{x\ln(\frac{2+\cos x}{3})} = 1 + x\ln(\frac{2+\cos x}{3}) + \frac{x^2\ln^2(\frac{2+\cos x}{3})}{2!} + \cdots$$
步骤 3:代入并简化
将上述展开式代入原极限表达式中,我们得到:
$$\lim _{x\rightarrow 0}\dfrac {1}{{x}^{3}}[1 + x\ln(\frac{2+\cos x}{3}) + \frac{x^2\ln^2(\frac{2+\cos x}{3})}{2!} + \cdots - 1]$$
$$= \lim _{x\rightarrow 0}\dfrac {1}{{x}^{3}}[x\ln(\frac{2+\cos x}{3}) + \frac{x^2\ln^2(\frac{2+\cos x}{3})}{2!} + \cdots]$$
$$= \lim _{x\rightarrow 0}\dfrac {1}{{x}^{2}}[\ln(\frac{2+\cos x}{3}) + \frac{x\ln^2(\frac{2+\cos x}{3})}{2!} + \cdots]$$
步骤 4:利用洛必达法则
由于上述极限表达式在$x\rightarrow 0$时为$\frac{0}{0}$型,我们使用洛必达法则求解。对分子和分母分别求导,我们得到:
$$\lim _{x\rightarrow 0}\dfrac {1}{{x}^{2}}[\ln(\frac{2+\cos x}{3}) + \frac{x\ln^2(\frac{2+\cos x}{3})}{2!} + \cdots]$$
$$= \lim _{x\rightarrow 0}\dfrac {\frac{-\sin x}{2+\cos x}}{2x}$$
$$= -\frac{1}{2}\lim _{x\rightarrow 0}\dfrac {\sin x}{x}\lim _{x\rightarrow 0}\dfrac {1}{2+\cos x}$$
$$= -\frac{1}{2}\times 1\times \frac{1}{2+\cos 0}$$
$$= -\frac{1}{2}\times 1\times \frac{1}{3}$$
$$= -\frac{1}{6}$$
首先,我们注意到极限表达式中包含指数函数和多项式。为了简化问题,我们使用对数的性质,将指数函数转化为对数形式。具体地,我们有:
$$\lim _{x\rightarrow 0}\dfrac {1}{{x}^{3}}[ {(\dfrac {2+\cos x}{3})}^{x}-1] = \lim _{x\rightarrow 0}\dfrac {1}{{x}^{3}}[e^{x\ln(\frac{2+\cos x}{3})}-1]$$
步骤 2:利用泰勒展开
接下来,我们利用$e^y$的泰勒展开式,其中$y=x\ln(\frac{2+\cos x}{3})$。泰勒展开式为:
$$e^y = 1 + y + \frac{y^2}{2!} + \frac{y^3}{3!} + \cdots$$
因此,我们有:
$$e^{x\ln(\frac{2+\cos x}{3})} = 1 + x\ln(\frac{2+\cos x}{3}) + \frac{x^2\ln^2(\frac{2+\cos x}{3})}{2!} + \cdots$$
步骤 3:代入并简化
将上述展开式代入原极限表达式中,我们得到:
$$\lim _{x\rightarrow 0}\dfrac {1}{{x}^{3}}[1 + x\ln(\frac{2+\cos x}{3}) + \frac{x^2\ln^2(\frac{2+\cos x}{3})}{2!} + \cdots - 1]$$
$$= \lim _{x\rightarrow 0}\dfrac {1}{{x}^{3}}[x\ln(\frac{2+\cos x}{3}) + \frac{x^2\ln^2(\frac{2+\cos x}{3})}{2!} + \cdots]$$
$$= \lim _{x\rightarrow 0}\dfrac {1}{{x}^{2}}[\ln(\frac{2+\cos x}{3}) + \frac{x\ln^2(\frac{2+\cos x}{3})}{2!} + \cdots]$$
步骤 4:利用洛必达法则
由于上述极限表达式在$x\rightarrow 0$时为$\frac{0}{0}$型,我们使用洛必达法则求解。对分子和分母分别求导,我们得到:
$$\lim _{x\rightarrow 0}\dfrac {1}{{x}^{2}}[\ln(\frac{2+\cos x}{3}) + \frac{x\ln^2(\frac{2+\cos x}{3})}{2!} + \cdots]$$
$$= \lim _{x\rightarrow 0}\dfrac {\frac{-\sin x}{2+\cos x}}{2x}$$
$$= -\frac{1}{2}\lim _{x\rightarrow 0}\dfrac {\sin x}{x}\lim _{x\rightarrow 0}\dfrac {1}{2+\cos x}$$
$$= -\frac{1}{2}\times 1\times \frac{1}{2+\cos 0}$$
$$= -\frac{1}{2}\times 1\times \frac{1}{3}$$
$$= -\frac{1}{6}$$