题目
证明方程^4+4x-3=0 在 ^4+4x-3=0 内至少有一个实根。
证明方程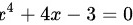
在 
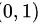内至少有一个实根。
题目解答
答案
因为方程 ；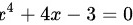
令函数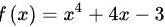
，根据基本函数求导公式对其求导得：
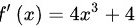
在 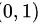内 ,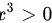 
，
所以导数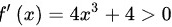
所以该区间为单调递增区间；
又因为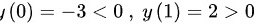
所以在区间 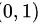内必定存在一个点使得：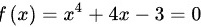
即方程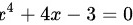 在 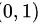内至少有一个实根。
故本题证明成立。
解析
步骤 1：定义函数
定义函数$f(x)={x}^{4}+4x-3$，该函数在区间(0,1)内连续。
步骤 2：求导数
求函数$f(x)$的导数$f'(x)=4{x}^{3}+4$。
步骤 3：分析导数的符号
在区间(0,1)内，$x^3 > 0$，因此$f'(x)=4{x}^{3}+4 > 0$，说明$f(x)$在(0,1)内是单调递增的。
步骤 4：计算端点值
计算$f(0)=-3$和$f(1)=2$。
步骤 5：应用介值定理
由于$f(x)$在(0,1)内连续且单调递增，且$f(0) < 0$，$f(1) > 0$，根据介值定理，存在$c \in (0,1)$，使得$f(c)=0$。
定义函数$f(x)={x}^{4}+4x-3$，该函数在区间(0,1)内连续。
步骤 2：求导数
求函数$f(x)$的导数$f'(x)=4{x}^{3}+4$。
步骤 3：分析导数的符号
在区间(0,1)内，$x^3 > 0$，因此$f'(x)=4{x}^{3}+4 > 0$，说明$f(x)$在(0,1)内是单调递增的。
步骤 4：计算端点值
计算$f(0)=-3$和$f(1)=2$。
步骤 5：应用介值定理
由于$f(x)$在(0,1)内连续且单调递增，且$f(0) < 0$，$f(1) > 0$，根据介值定理，存在$c \in (0,1)$，使得$f(c)=0$。