题目
(2017)求极限 lim _(xarrow infty )dfrac (2x-sin x)(x+sin x)
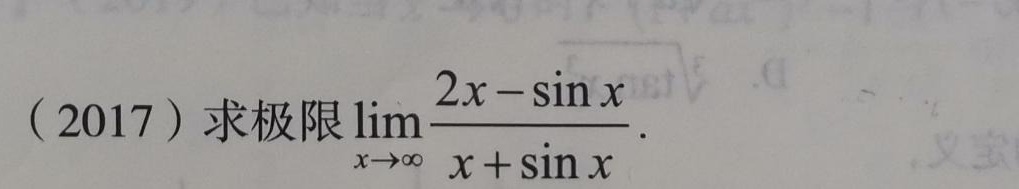
题目解答
答案

解析
步骤 1:将分子和分母同时除以x
将极限表达式中的分子和分母同时除以x,得到 $\lim _{x\rightarrow \infty }\dfrac {2-\dfrac {\sin x}{x}}{1+\dfrac {\sin x}{x}}$。
步骤 2:分析 $\dfrac {\sin x}{x}$ 的极限
当 $x\rightarrow \infty$ 时,$\dfrac {\sin x}{x}\rightarrow 0$,因为 $\sin x$ 的值在 $[-1,1]$ 之间,而分母 $x$ 趋于无穷大,所以 $\dfrac {\sin x}{x}$ 趋于0。
步骤 3:计算极限
将 $\dfrac {\sin x}{x}$ 的极限值代入步骤1得到的表达式中,得到 $\lim _{x\rightarrow \infty }\dfrac {2-\dfrac {\sin x}{x}}{1+\dfrac {\sin x}{x}} = \dfrac {2-0}{1+0} = 2$。
将极限表达式中的分子和分母同时除以x,得到 $\lim _{x\rightarrow \infty }\dfrac {2-\dfrac {\sin x}{x}}{1+\dfrac {\sin x}{x}}$。
步骤 2:分析 $\dfrac {\sin x}{x}$ 的极限
当 $x\rightarrow \infty$ 时,$\dfrac {\sin x}{x}\rightarrow 0$,因为 $\sin x$ 的值在 $[-1,1]$ 之间,而分母 $x$ 趋于无穷大,所以 $\dfrac {\sin x}{x}$ 趋于0。
步骤 3:计算极限
将 $\dfrac {\sin x}{x}$ 的极限值代入步骤1得到的表达式中,得到 $\lim _{x\rightarrow \infty }\dfrac {2-\dfrac {\sin x}{x}}{1+\dfrac {\sin x}{x}} = \dfrac {2-0}{1+0} = 2$。