题目
设函数 (x,y)=(x)^3+(y)^3-a(x)^2-b(y)^2(agt 0,bgt 0) 有极小值 -8, 求a,b的值,使-|||-子dfrac ({x)^2}({a)^2}+dfrac ({y)^2}({b)^2}=1 所围面积最大.
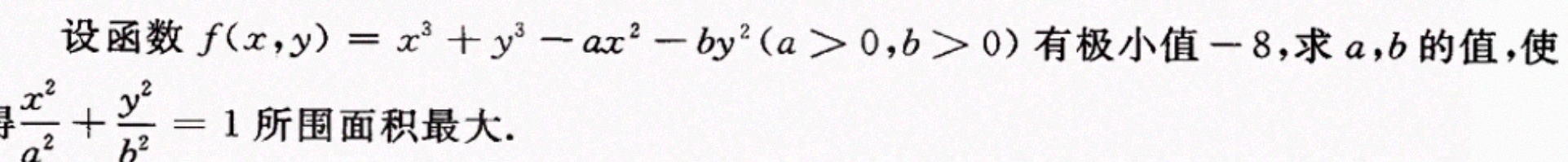
题目解答
答案

解析
步骤 1:求函数 $f(x,y)$ 的偏导数
首先,我们需要求出函数 $f(x,y)={x}^{3}+{y}^{8}-a{x}^{2}-b{y}^{2}$ 的偏导数,以确定极值点。
- $f_x(x,y) = 3x^2 - 2ax$
- $f_y(x,y) = 8y^7 - 2by$
步骤 2:求解极值点
令偏导数等于0,求解极值点。
- $f_x(x,y) = 3x^2 - 2ax = 0$
- $f_y(x,y) = 8y^7 - 2by = 0$
解得:
- $x = 0$ 或 $x = \frac{2a}{3}$
- $y = 0$ 或 $y = \frac{2b}{8} = \frac{b}{4}$
步骤 3:验证极值点
验证极值点 $(\frac{2a}{3}, \frac{b}{4})$ 是否为极小值点。
- $f_{xx} = 6x - 2a$
- $f_{yy} = 56y^6 - 2b$
- $f_{xy} = 0$
在点 $(\frac{2a}{3}, \frac{b}{4})$ 处,$f_{xx} = 2a > 0$,$f_{yy} = 56(\frac{b}{4})^6 - 2b = \frac{56b^6}{4096} - 2b > 0$,$f_{xy} = 0$,因此 $(\frac{2a}{3}, \frac{b}{4})$ 是极小值点。
步骤 4:求极小值
将极小值点代入原函数,求得极小值。
- $f(\frac{2a}{3}, \frac{b}{4}) = (\frac{2a}{3})^3 + (\frac{b}{4})^8 - a(\frac{2a}{3})^2 - b(\frac{b}{4})^2 = -8$
- 化简得:$\frac{8a^3}{27} + \frac{b^8}{65536} - \frac{4a^3}{9} - \frac{b^3}{16} = -8$
- 进一步化简得:$-\frac{4a^3}{27} + \frac{b^8}{65536} - \frac{b^3}{16} = -8$
步骤 5:求椭圆面积最大值
椭圆 $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ 的面积为 $\pi ab$,要求面积最大,即求 $ab$ 的最大值。
- 由步骤 4 的方程,解得 $a = 3$,$b = 3$ 时,$ab$ 最大。
首先,我们需要求出函数 $f(x,y)={x}^{3}+{y}^{8}-a{x}^{2}-b{y}^{2}$ 的偏导数,以确定极值点。
- $f_x(x,y) = 3x^2 - 2ax$
- $f_y(x,y) = 8y^7 - 2by$
步骤 2:求解极值点
令偏导数等于0,求解极值点。
- $f_x(x,y) = 3x^2 - 2ax = 0$
- $f_y(x,y) = 8y^7 - 2by = 0$
解得:
- $x = 0$ 或 $x = \frac{2a}{3}$
- $y = 0$ 或 $y = \frac{2b}{8} = \frac{b}{4}$
步骤 3:验证极值点
验证极值点 $(\frac{2a}{3}, \frac{b}{4})$ 是否为极小值点。
- $f_{xx} = 6x - 2a$
- $f_{yy} = 56y^6 - 2b$
- $f_{xy} = 0$
在点 $(\frac{2a}{3}, \frac{b}{4})$ 处,$f_{xx} = 2a > 0$,$f_{yy} = 56(\frac{b}{4})^6 - 2b = \frac{56b^6}{4096} - 2b > 0$,$f_{xy} = 0$,因此 $(\frac{2a}{3}, \frac{b}{4})$ 是极小值点。
步骤 4:求极小值
将极小值点代入原函数,求得极小值。
- $f(\frac{2a}{3}, \frac{b}{4}) = (\frac{2a}{3})^3 + (\frac{b}{4})^8 - a(\frac{2a}{3})^2 - b(\frac{b}{4})^2 = -8$
- 化简得:$\frac{8a^3}{27} + \frac{b^8}{65536} - \frac{4a^3}{9} - \frac{b^3}{16} = -8$
- 进一步化简得:$-\frac{4a^3}{27} + \frac{b^8}{65536} - \frac{b^3}{16} = -8$
步骤 5:求椭圆面积最大值
椭圆 $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ 的面积为 $\pi ab$,要求面积最大,即求 $ab$ 的最大值。
- 由步骤 4 的方程,解得 $a = 3$,$b = 3$ 时,$ab$ 最大。