题目
160 求极限lim _(xarrow infty )(x)^2[ ln ((x)^2+1)-2ln x] = x]=
160 求极限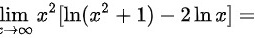
题目解答
答案
解:
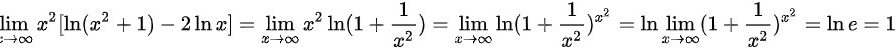
解析
步骤 1:化简表达式
首先,我们化简给定的表达式。利用对数的性质,我们可以将表达式中的对数项合并。
$$
\ln(x^2 + 1) - 2\ln x = \ln(x^2 + 1) - \ln(x^2) = \ln\left(\frac{x^2 + 1}{x^2}\right) = \ln\left(1 + \frac{1}{x^2}\right)
$$
步骤 2:代入化简后的表达式
将化简后的表达式代入原极限中,得到:
$$
\lim_{x \to \infty} x^2 \ln\left(1 + \frac{1}{x^2}\right)
$$
步骤 3:利用等价无穷小替换
当$x \to \infty$时,$\frac{1}{x^2} \to 0$,因此可以利用等价无穷小替换$\ln(1 + u) \sim u$(当$u \to 0$时),得到:
$$
\lim_{x \to \infty} x^2 \cdot \frac{1}{x^2} = \lim_{x \to \infty} 1 = 1
$$
首先,我们化简给定的表达式。利用对数的性质,我们可以将表达式中的对数项合并。
$$
\ln(x^2 + 1) - 2\ln x = \ln(x^2 + 1) - \ln(x^2) = \ln\left(\frac{x^2 + 1}{x^2}\right) = \ln\left(1 + \frac{1}{x^2}\right)
$$
步骤 2:代入化简后的表达式
将化简后的表达式代入原极限中,得到:
$$
\lim_{x \to \infty} x^2 \ln\left(1 + \frac{1}{x^2}\right)
$$
步骤 3:利用等价无穷小替换
当$x \to \infty$时,$\frac{1}{x^2} \to 0$,因此可以利用等价无穷小替换$\ln(1 + u) \sim u$(当$u \to 0$时),得到:
$$
\lim_{x \to \infty} x^2 \cdot \frac{1}{x^2} = \lim_{x \to \infty} 1 = 1
$$