题目
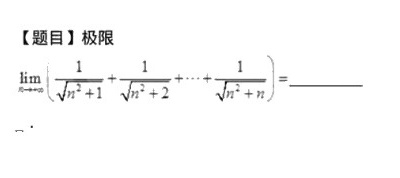
[题目]极限-|||-lim _(narrow infty )(dfrac (1)(sqrt {{n)^2+1}}+dfrac (1)(sqrt {{n)^2+2}}+... +dfrac (1)(sqrt {{n)^2+n}})= __
题目解答
答案

解析
步骤 1:确定极限表达式的结构
给定的极限表达式为 $\lim _{n\rightarrow \infty }(\dfrac {1}{\sqrt {{n}^{2}+1}}+\dfrac {1}{\sqrt {{n}^{2}+2}}+\cdots +\dfrac {1}{\sqrt {{n}^{2}+n}})$。这是一个求和表达式,其中每一项都是分母为 $\sqrt{n^2+k}$ 的倒数,$k$ 从 1 到 $n$。
步骤 2:分析每一项的极限行为
当 $n$ 趋于无穷大时,每一项 $\dfrac {1}{\sqrt {{n}^{2}+k}}$ 都趋于 $\dfrac {1}{n}$,因为 $\sqrt{n^2+k}$ 趋于 $n$。因此,每一项都趋于 $\dfrac {1}{n}$。
步骤 3:求和并取极限
由于有 $n$ 项,每项都趋于 $\dfrac {1}{n}$,所以整个求和表达式趋于 $n \times \dfrac {1}{n} = 1$。因此,原极限表达式等于 1。
给定的极限表达式为 $\lim _{n\rightarrow \infty }(\dfrac {1}{\sqrt {{n}^{2}+1}}+\dfrac {1}{\sqrt {{n}^{2}+2}}+\cdots +\dfrac {1}{\sqrt {{n}^{2}+n}})$。这是一个求和表达式,其中每一项都是分母为 $\sqrt{n^2+k}$ 的倒数,$k$ 从 1 到 $n$。
步骤 2:分析每一项的极限行为
当 $n$ 趋于无穷大时,每一项 $\dfrac {1}{\sqrt {{n}^{2}+k}}$ 都趋于 $\dfrac {1}{n}$,因为 $\sqrt{n^2+k}$ 趋于 $n$。因此,每一项都趋于 $\dfrac {1}{n}$。
步骤 3:求和并取极限
由于有 $n$ 项,每项都趋于 $\dfrac {1}{n}$,所以整个求和表达式趋于 $n \times \dfrac {1}{n} = 1$。因此,原极限表达式等于 1。