题目
lim _(xarrow 1)dfrac (1-{x)^3}(1-x)
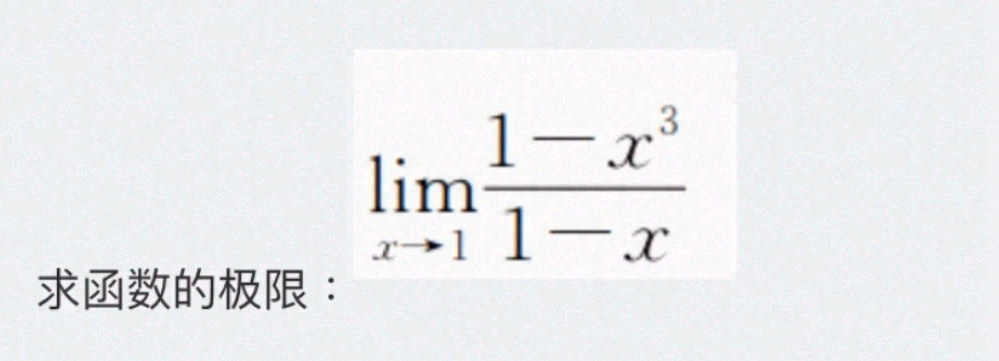
题目解答
答案

解析
步骤 1:因式分解
首先,我们注意到分子 $1 - x^3$ 可以通过立方差公式进行因式分解。立方差公式为 $a^3 - b^3 = (a - b)(a^2 + ab + b^2)$。在这个问题中,$a = 1$,$b = x$,因此 $1 - x^3 = (1 - x)(1^2 + 1 \cdot x + x^2) = (1 - x)(1 + x + x^2)$。
步骤 2:简化表达式
将因式分解后的分子代入原极限表达式中,得到 $\lim _{x\rightarrow 1}\dfrac {(1-x)(1+x+{x}^{2})}{1-x}$。由于 $x \neq 1$,我们可以约去分子和分母中的 $(1 - x)$,得到 $\lim _{x\rightarrow 1}(1+x+{x}^{2})$。
步骤 3:计算极限
现在,我们只需要计算 $1 + x + x^2$ 在 $x$ 趋向于 $1$ 时的极限。将 $x = 1$ 代入表达式中,得到 $1 + 1 + 1^2 = 3$。
首先,我们注意到分子 $1 - x^3$ 可以通过立方差公式进行因式分解。立方差公式为 $a^3 - b^3 = (a - b)(a^2 + ab + b^2)$。在这个问题中,$a = 1$,$b = x$,因此 $1 - x^3 = (1 - x)(1^2 + 1 \cdot x + x^2) = (1 - x)(1 + x + x^2)$。
步骤 2:简化表达式
将因式分解后的分子代入原极限表达式中,得到 $\lim _{x\rightarrow 1}\dfrac {(1-x)(1+x+{x}^{2})}{1-x}$。由于 $x \neq 1$,我们可以约去分子和分母中的 $(1 - x)$,得到 $\lim _{x\rightarrow 1}(1+x+{x}^{2})$。
步骤 3:计算极限
现在,我们只需要计算 $1 + x + x^2$ 在 $x$ 趋向于 $1$ 时的极限。将 $x = 1$ 代入表达式中,得到 $1 + 1 + 1^2 = 3$。