题目
(6) lim _(narrow infty )dfrac ({5)^n-(3)^n}({5)^n+(2)^n}
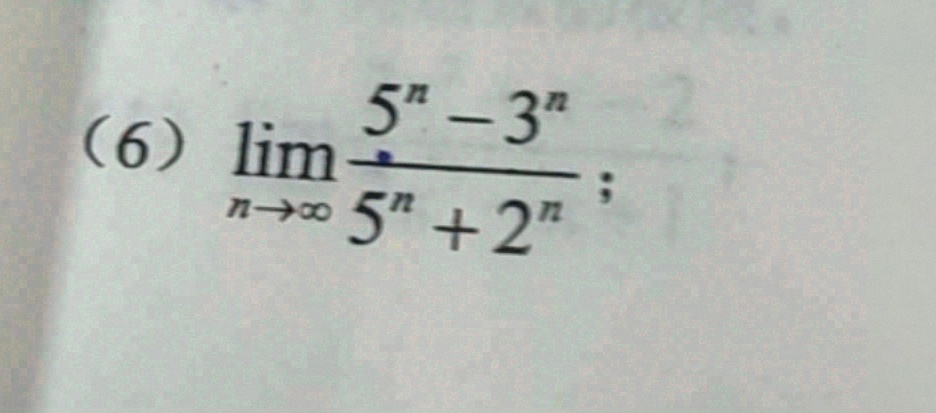
题目解答
答案
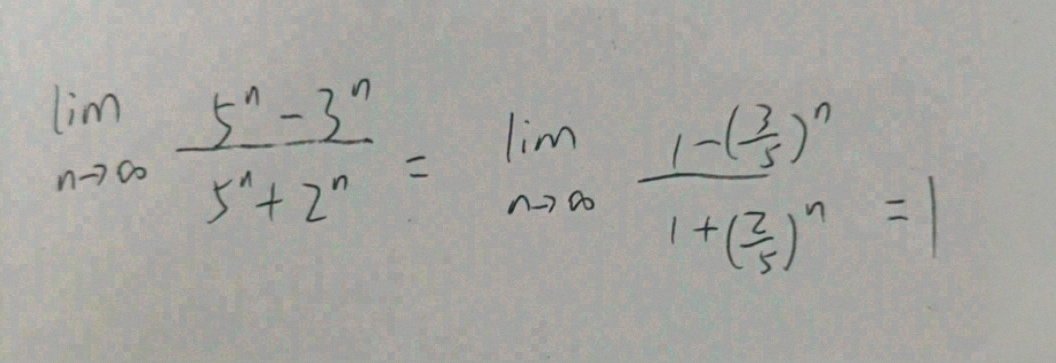
解析
考查要点:本题主要考查指数函数的极限性质以及无穷大时不同底数指数函数的增长比较。
解题核心思路:
当$n \rightarrow \infty$时,分子和分母中的主导项均为$5^n$。通过将分子和分母同时除以$5^n$,可以将原式转化为关于$(3/5)^n$和$(2/5)^n$的表达式。由于$0 < 3/5 < 1$和$0 < 2/5 < 1$,根据指数函数极限性质,当$n \rightarrow \infty$时,$(3/5)^n \rightarrow 0$,$(2/5)^n \rightarrow 0$,从而简化求极限过程。
破题关键点:
- 提取主导项:分子和分母均提取$5^n$,简化表达式。
- 利用极限性质:将问题转化为关于$(3/5)^n$和$(2/5)^n$的极限计算。
步骤1:分子分母同除以$5^n$
原式可变形为:
$\lim_{n \rightarrow \infty} \frac{5^n - 3^n}{5^n + 2^n} = \lim_{n \rightarrow \infty} \frac{1 - \left(\frac{3}{5}\right)^n}{1 + \left(\frac{2}{5}\right)^n}$
步骤2:分析极限趋势
- 分子中的$\left(\frac{3}{5}\right)^n$:由于$\frac{3}{5} < 1$,当$n \rightarrow \infty$时,$\left(\frac{3}{5}\right)^n \rightarrow 0$。
- 分母中的$\left(\frac{2}{5}\right)^n$:由于$\frac{2}{5} < 1$,当$n \rightarrow \infty$时,$\left(\frac{2}{5}\right)^n \rightarrow 0$。
步骤3:代入极限值
将上述结果代入变形后的表达式:
$\lim_{n \rightarrow \infty} \frac{1 - 0}{1 + 0} = \frac{1}{1} = 1$