题目
27.已知方程 ^4+2(x)^3-3(x)^2-4x+a=0 有两个重根,则 a=
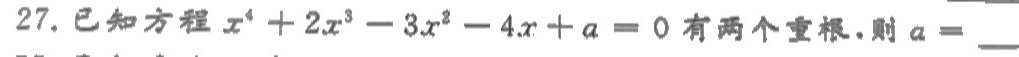
题目解答
答案

解析
步骤 1:确定方程的重根形式
由于方程 ${x}^{4}+2{x}^{3}-3{x}^{2}-4x+a=0$ 有两个重根,我们可以假设方程可以写成两个二次多项式的平方形式,即
${({x}^{2}+bx+c)}^{2}=0$。
步骤 2:展开并比较系数
将 ${({x}^{2}+bx+c)}^{2}$ 展开,得到
${x}^{4}+2b{x}^{3}+({b}^{2}+2c){x}^{2}+2bcx+{c}^{2}=0$。
将上述展开式与原方程 ${x}^{4}+2{x}^{3}-3{x}^{2}-4x+a=0$ 比较系数,得到
$2b=2$,
${b}^{2}+2c=-3$,
$2bc=-4$,
${c}^{2}=a$。
步骤 3:求解方程组
从 $2b=2$ 可得 $b=1$。
将 $b=1$ 代入 ${b}^{2}+2c=-3$,得到 $1+2c=-3$,解得 $c=-2$。
将 $b=1$ 和 $c=-2$ 代入 $2bc=-4$,验证等式成立。
最后,将 $c=-2$ 代入 ${c}^{2}=a$,得到 $a=4$。
由于方程 ${x}^{4}+2{x}^{3}-3{x}^{2}-4x+a=0$ 有两个重根,我们可以假设方程可以写成两个二次多项式的平方形式,即
${({x}^{2}+bx+c)}^{2}=0$。
步骤 2:展开并比较系数
将 ${({x}^{2}+bx+c)}^{2}$ 展开,得到
${x}^{4}+2b{x}^{3}+({b}^{2}+2c){x}^{2}+2bcx+{c}^{2}=0$。
将上述展开式与原方程 ${x}^{4}+2{x}^{3}-3{x}^{2}-4x+a=0$ 比较系数,得到
$2b=2$,
${b}^{2}+2c=-3$,
$2bc=-4$,
${c}^{2}=a$。
步骤 3:求解方程组
从 $2b=2$ 可得 $b=1$。
将 $b=1$ 代入 ${b}^{2}+2c=-3$,得到 $1+2c=-3$,解得 $c=-2$。
将 $b=1$ 和 $c=-2$ 代入 $2bc=-4$,验证等式成立。
最后,将 $c=-2$ 代入 ${c}^{2}=a$,得到 $a=4$。