题目
2.求曲线 y={t)^2(t-1) . 在 t=2 处的切线方程与法线方程
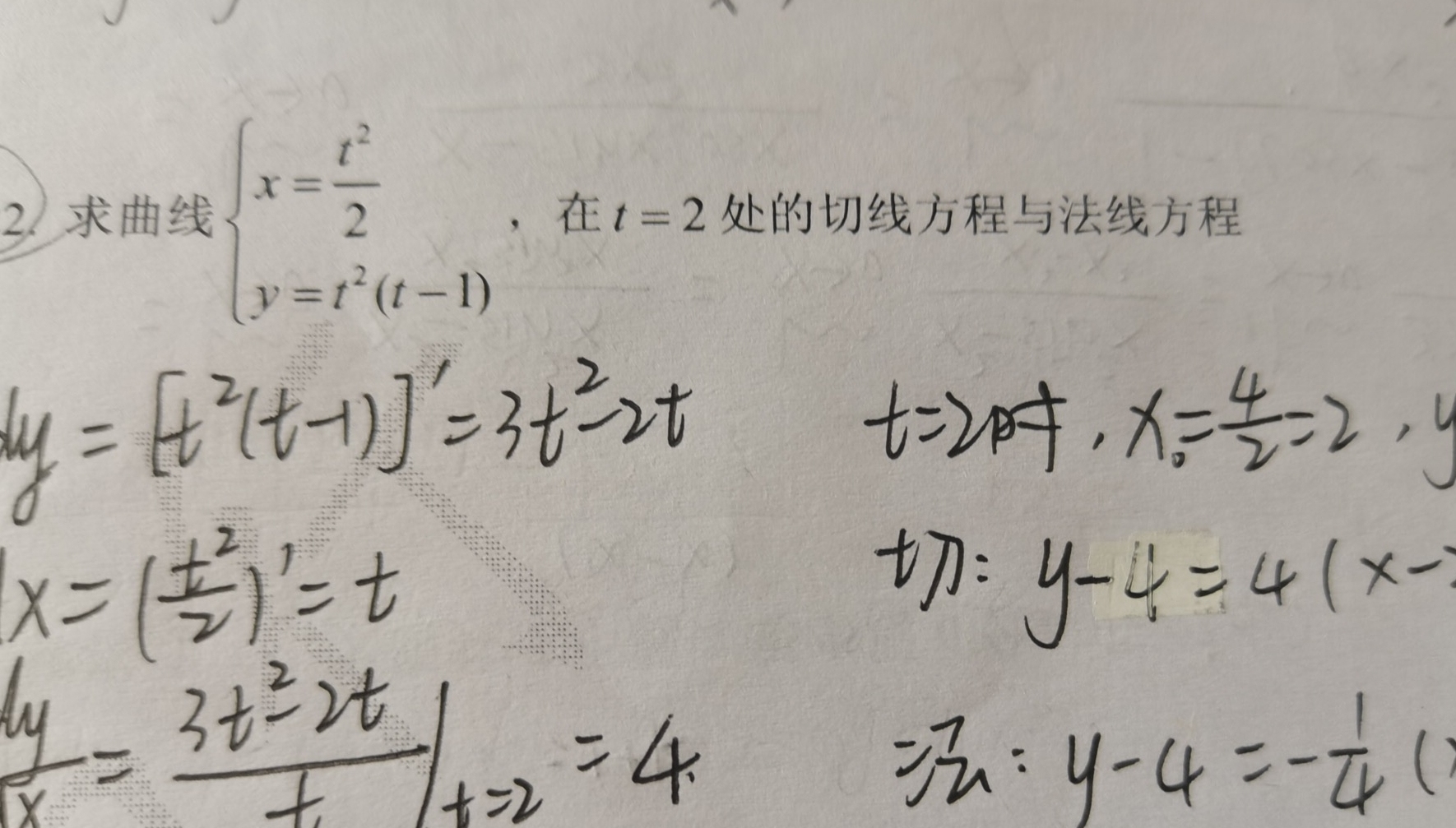
题目解答
答案

解析
步骤 1:求导数
首先,我们需要求出曲线在参数 $t$ 下的导数。给定的参数方程为:
$$
\begin{cases}
x = \frac{t^2}{2} \\
y = t^2(t-1)
\end{cases}
$$
对 $x$ 和 $y$ 分别求导,得到:
$$
\begin{cases}
\frac{dx}{dt} = t \\
\frac{dy}{dt} = 3t^2 - 2t
\end{cases}
$$
步骤 2:求切线斜率
切线斜率 $k$ 为 $\frac{dy}{dx}$,即:
$$
k = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{3t^2 - 2t}{t} = 3t - 2
$$
当 $t = 2$ 时,切线斜率为:
$$
k = 3 \cdot 2 - 2 = 4
$$
步骤 3:求切点坐标
当 $t = 2$ 时,代入参数方程求得切点坐标:
$$
\begin{cases}
x = \frac{2^2}{2} = 2 \\
y = 2^2(2-1) = 4
\end{cases}
$$
步骤 4:求切线方程
切线方程为:
$$
y - y_0 = k(x - x_0)
$$
代入切点坐标 $(2, 4)$ 和斜率 $k = 4$,得到:
$$
y - 4 = 4(x - 2)
$$
化简得:
$$
4x - y - 4 = 0
$$
步骤 5:求法线方程
法线斜率为切线斜率的负倒数,即:
$$
k_{\text{法线}} = -\frac{1}{k} = -\frac{1}{4}
$$
法线方程为:
$$
y - y_0 = k_{\text{法线}}(x - x_0)
$$
代入切点坐标 $(2, 4)$ 和法线斜率 $k_{\text{法线}} = -\frac{1}{4}$,得到:
$$
y - 4 = -\frac{1}{4}(x - 2)
$$
化简得:
$$
x - 4y + 14 = 0
$$
首先,我们需要求出曲线在参数 $t$ 下的导数。给定的参数方程为:
$$
\begin{cases}
x = \frac{t^2}{2} \\
y = t^2(t-1)
\end{cases}
$$
对 $x$ 和 $y$ 分别求导,得到:
$$
\begin{cases}
\frac{dx}{dt} = t \\
\frac{dy}{dt} = 3t^2 - 2t
\end{cases}
$$
步骤 2:求切线斜率
切线斜率 $k$ 为 $\frac{dy}{dx}$,即:
$$
k = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{3t^2 - 2t}{t} = 3t - 2
$$
当 $t = 2$ 时,切线斜率为:
$$
k = 3 \cdot 2 - 2 = 4
$$
步骤 3:求切点坐标
当 $t = 2$ 时,代入参数方程求得切点坐标:
$$
\begin{cases}
x = \frac{2^2}{2} = 2 \\
y = 2^2(2-1) = 4
\end{cases}
$$
步骤 4:求切线方程
切线方程为:
$$
y - y_0 = k(x - x_0)
$$
代入切点坐标 $(2, 4)$ 和斜率 $k = 4$,得到:
$$
y - 4 = 4(x - 2)
$$
化简得:
$$
4x - y - 4 = 0
$$
步骤 5:求法线方程
法线斜率为切线斜率的负倒数,即:
$$
k_{\text{法线}} = -\frac{1}{k} = -\frac{1}{4}
$$
法线方程为:
$$
y - y_0 = k_{\text{法线}}(x - x_0)
$$
代入切点坐标 $(2, 4)$ 和法线斜率 $k_{\text{法线}} = -\frac{1}{4}$,得到:
$$
y - 4 = -\frac{1}{4}(x - 2)
$$
化简得:
$$
x - 4y + 14 = 0
$$