题目
=dfrac (2x)(sqrt {2-x)}+ln (1+x)的定义域为______.
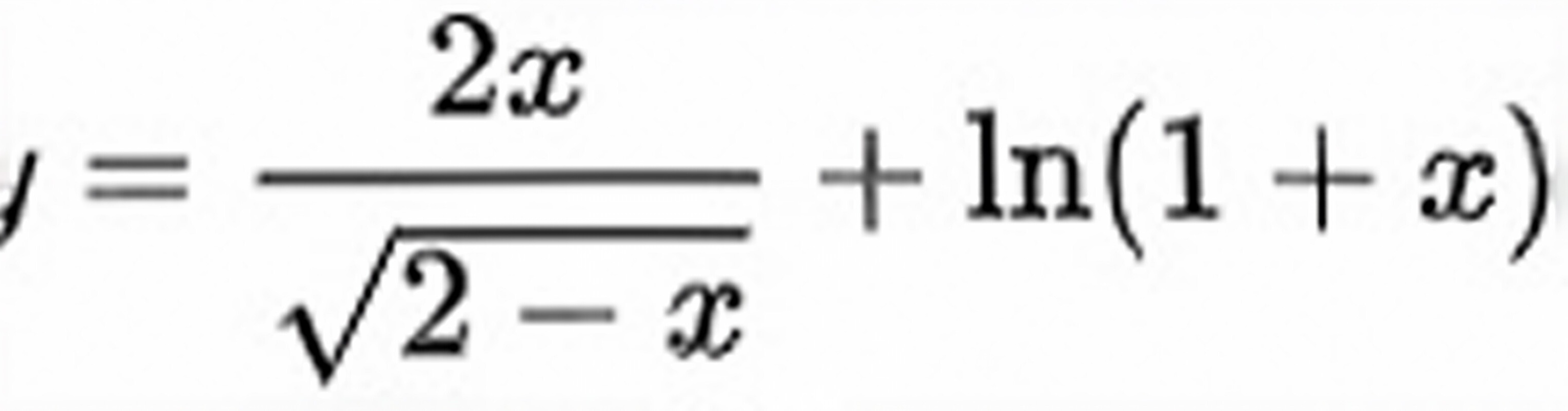 的定义域为______.
的定义域为______.
题目解答
答案
根据函数y的表达式,可以得到2-x>0,且1+x>0,综合两个不等式,可以得到x的取值范围是-1
解析
考查要点:本题主要考查函数定义域的求解,涉及分式、根号及对数函数的定义条件。
解题核心思路:
- 分式部分:分母中的根号表达式必须满足被开方数大于0,且分母不能为0。
- 对数部分:对数函数的真数必须大于0。
- 综合条件:将各部分的定义域取交集,得到最终结果。
破题关键点:
- 分式分母 $\sqrt{2-x}$ 的存在要求 $2-x > 0$。
- 对数函数 $\ln(1+x)$ 的存在要求 $1+x > 0$。
- 联立不等式,求出同时满足两个条件的 $x$ 范围。
-
分式部分 $\dfrac{2x}{\sqrt{2-x}}$ 的定义域
- 根号内的表达式必须大于0:
$2 - x > 0 \quad \Rightarrow \quad x < 2.$ - 分母 $\sqrt{2-x}$ 不能为0,但 $2-x > 0$ 已隐含此条件,无需额外限制。
- 根号内的表达式必须大于0:
-
对数部分 $\ln(1+x)$ 的定义域
- 真数必须大于0:
$1 + x > 0 \quad \Rightarrow \quad x > -1.$
- 真数必须大于0:
-
求交集
- 分式部分要求 $x < 2$,对数部分要求 $x > -1$。
- 综合得:
$-1 < x < 2.$