题目
lim _(xarrow dfrac {pi )(2)}dfrac (ln sin x)({(pi -2x))^2}.
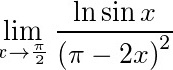 .
. 题目解答
答案
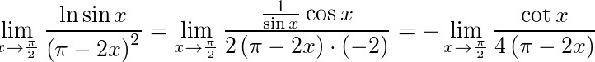
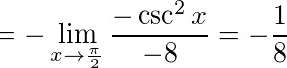
解析
步骤 1:应用洛必达法则
由于当$x\rightarrow \dfrac {\pi }{2}$时,$\ln \sin x$和${(\pi -2x)}^{2}$都趋于0,因此原极限是$\dfrac{0}{0}$型的不定式。我们可以应用洛必达法则,即对分子和分母分别求导,再求极限。
步骤 2:求导
对分子$\ln \sin x$求导,得到$\dfrac{1}{\sin x} \cdot \cos x = \cot x$。
对分母${(\pi -2x)}^{2}$求导,得到$2(\pi -2x) \cdot (-2) = -4(\pi -2x)$。
步骤 3:再次应用洛必达法则
由于求导后得到的极限仍然是$\dfrac{0}{0}$型的不定式,我们再次应用洛必达法则。
对分子$\cot x$求导,得到$-\csc^2 x$。
对分母$-4(\pi -2x)$求导,得到$-4 \cdot (-2) = 8$。
步骤 4:计算极限
现在我们有$\lim _{x\rightarrow \dfrac {\pi }{2}}\dfrac {-\csc^2 x}{8}$。当$x\rightarrow \dfrac {\pi }{2}$时,$\csc x = \dfrac{1}{\sin x}$趋于1,因此$\csc^2 x$趋于1。所以,原极限等于$\dfrac{-1}{8}$。
由于当$x\rightarrow \dfrac {\pi }{2}$时,$\ln \sin x$和${(\pi -2x)}^{2}$都趋于0,因此原极限是$\dfrac{0}{0}$型的不定式。我们可以应用洛必达法则,即对分子和分母分别求导,再求极限。
步骤 2:求导
对分子$\ln \sin x$求导,得到$\dfrac{1}{\sin x} \cdot \cos x = \cot x$。
对分母${(\pi -2x)}^{2}$求导,得到$2(\pi -2x) \cdot (-2) = -4(\pi -2x)$。
步骤 3:再次应用洛必达法则
由于求导后得到的极限仍然是$\dfrac{0}{0}$型的不定式,我们再次应用洛必达法则。
对分子$\cot x$求导,得到$-\csc^2 x$。
对分母$-4(\pi -2x)$求导,得到$-4 \cdot (-2) = 8$。
步骤 4:计算极限
现在我们有$\lim _{x\rightarrow \dfrac {\pi }{2}}\dfrac {-\csc^2 x}{8}$。当$x\rightarrow \dfrac {\pi }{2}$时,$\csc x = \dfrac{1}{\sin x}$趋于1,因此$\csc^2 x$趋于1。所以,原极限等于$\dfrac{-1}{8}$。