题目
某商店开业免费分发冰淇淋,现在还有6个口味不同的冰淇淋,店内有2名女孩和1名男孩,现将6个冰淇淋分配给这3个人,若每人至少分1个,则共有( )种不同的分法.A 280 B 320C 392 D 445 E 540
某商店开业免费分发冰淇淋,现在还有6个口味不同的冰淇淋,店内有2名女孩和1名男孩,现将6个冰淇淋分配给这3个人,若每人至少分1个,则共有( )种不同的分法.
A 280
B 320
C 392
D 445
E 540
题目解答
答案
将6个口味不同的冰淇淋分给3个人,每人至少分1个,可以用插板法来解决。
把6个冰淇淋排成一排,中间有5个间隔。
现在用2个板子插入这5个间隔中,将冰淇淋分成3份,对应分给3个人,这样的插板方法有 种。
种。
把6个冰淇淋分成1、1、4;1、2、3;2、2、2这三种情况。
当分成1、1、4时,有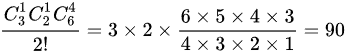 种分法。
种分法。
当分成1、2、3时,有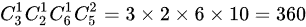 种分法。
种分法。
当分成2、2、2时,有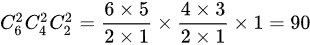 种分法。
种分法。
将三种情况的分法数相加,90+360+90=540种。
综上所述,答案:E.
解析
本题考查排列组合中的分组分配问题,核心思路是将不同口味的冰淇淋分成满足条件的组,再分配给不同的人。关键在于:
- 分类讨论:根据冰淇淋数量的分组情况(如1,1,4;1,2,3;2,2,2),分别计算每种情况的分法数。
- 排列组合公式:注意区分元素是否有序,以及是否需要消除重复计数(如相同组大小时需除以排列数)。
情况1:分组为1,1,4
- 选择得4个冰淇淋的人:有$C_3^1$种选择。
- 从6个中选4个:有$C_6^4$种方式。
- 分配剩余2个:将剩下的2个冰淇淋分给剩下的2人,每人1个,有$2!$种排列。
- 消除重复:由于两组均为1个,需除以$2!$(避免重复计数)。
分法数:
$C_3^1 \cdot C_6^4 \cdot \frac{2!}{2!} = 3 \cdot 15 \cdot 2 = 90$
情况2:分组为1,2,3
- 确定各组人数分配:选择得1个、2个、3个的人,有$3!$种排列。
- 分配冰淇淋:
- 选1个:$C_6^1$种。
- 选2个:$C_5^2$种(从剩余5个中选)。
- 剩余3个自动分配。
分法数:
$3! \cdot C_6^1 \cdot C_5^2 = 6 \cdot 6 \cdot 10 = 360$
情况3:分组为2,2,2
- 分组方式:将6个冰淇淋均分3组,每组2个,有$\frac{C_6^2 \cdot C_4^2}{3!}$种分法。
- 分配给3人:每组对应1人,有$3!$种排列。
分法数:
$\frac{C_6^2 \cdot C_4^2}{3!} \cdot 3! = 15 \cdot 6 = 90$
总分法数
将三种情况相加:
$90 + 360 + 90 = 540$