题目
26.设 (x)=dfrac (ln |x|)(|x-1|)sin x, 求f(x)的间断点并判断其类型.
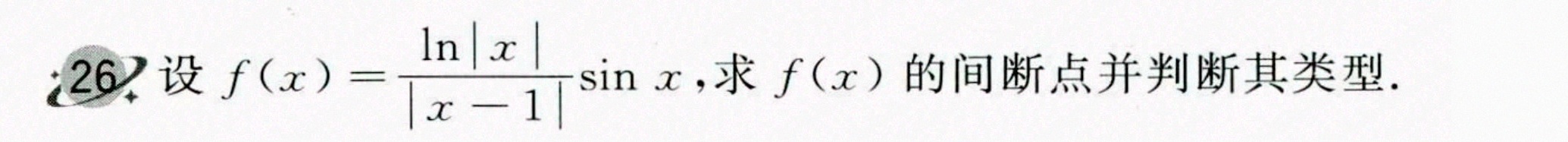
题目解答
答案

解析
步骤 1:确定函数的定义域
函数 $f(x)=\dfrac {\ln |x|}{|x-1|}\sin x$ 中,$\ln |x|$ 定义域为 $x \neq 0$,$|x-1|$ 定义域为 $x \neq 1$,因此函数的定义域为 $x \neq 0$ 且 $x \neq 1$。
步骤 2:判断间断点
由于函数在 $x=0$ 和 $x=1$ 处没有定义,因此这两个点是函数的间断点。
步骤 3:判断间断点类型
- 对于 $x=0$,计算 $\lim _{x\rightarrow 0}f(x)$。
- 对于 $x=1$,计算 $\lim _{x\rightarrow 1^-}f(x)$ 和 $\lim _{x\rightarrow 1^+}f(x)$。
步骤 4:计算 $\lim _{x\rightarrow 0}f(x)$
$$
\lim _{x\rightarrow 0}f(x)=\lim _{x\rightarrow 0}\dfrac {\ln |x|}{|x-1|}\sin x=\lim _{x\rightarrow 0}\dfrac {\ln |x|}{|x-1|}\cdot \lim _{x\rightarrow 0}\sin x=0
$$
因为 $\lim _{x\rightarrow 0}\sin x=0$,所以 $\lim _{x\rightarrow 0}f(x)=0$,因此 $x=0$ 是可去间断点。
步骤 5:计算 $\lim _{x\rightarrow 1^-}f(x)$ 和 $\lim _{x\rightarrow 1^+}f(x)$
$$
\lim _{x\rightarrow 1^-}f(x)=\lim _{x\rightarrow 1^-}\dfrac {\ln |x|}{|x-1|}\sin x=\lim _{x\rightarrow 1^-}\dfrac {\ln |x|}{1-x}\sin x=-\sin 1
$$
$$
\lim _{x\rightarrow 1^+}f(x)=\lim _{x\rightarrow 1^+}\dfrac {\ln |x|}{|x-1|}\sin x=\lim _{x\rightarrow 1^+}\dfrac {\ln |x|}{x-1}\sin x=\sin 1
$$
因为 $\lim _{x\rightarrow 1^-}f(x) \neq \lim _{x\rightarrow 1^+}f(x)$,所以 $x=1$ 是跳跃间断点。
函数 $f(x)=\dfrac {\ln |x|}{|x-1|}\sin x$ 中,$\ln |x|$ 定义域为 $x \neq 0$,$|x-1|$ 定义域为 $x \neq 1$,因此函数的定义域为 $x \neq 0$ 且 $x \neq 1$。
步骤 2:判断间断点
由于函数在 $x=0$ 和 $x=1$ 处没有定义,因此这两个点是函数的间断点。
步骤 3:判断间断点类型
- 对于 $x=0$,计算 $\lim _{x\rightarrow 0}f(x)$。
- 对于 $x=1$,计算 $\lim _{x\rightarrow 1^-}f(x)$ 和 $\lim _{x\rightarrow 1^+}f(x)$。
步骤 4:计算 $\lim _{x\rightarrow 0}f(x)$
$$
\lim _{x\rightarrow 0}f(x)=\lim _{x\rightarrow 0}\dfrac {\ln |x|}{|x-1|}\sin x=\lim _{x\rightarrow 0}\dfrac {\ln |x|}{|x-1|}\cdot \lim _{x\rightarrow 0}\sin x=0
$$
因为 $\lim _{x\rightarrow 0}\sin x=0$,所以 $\lim _{x\rightarrow 0}f(x)=0$,因此 $x=0$ 是可去间断点。
步骤 5:计算 $\lim _{x\rightarrow 1^-}f(x)$ 和 $\lim _{x\rightarrow 1^+}f(x)$
$$
\lim _{x\rightarrow 1^-}f(x)=\lim _{x\rightarrow 1^-}\dfrac {\ln |x|}{|x-1|}\sin x=\lim _{x\rightarrow 1^-}\dfrac {\ln |x|}{1-x}\sin x=-\sin 1
$$
$$
\lim _{x\rightarrow 1^+}f(x)=\lim _{x\rightarrow 1^+}\dfrac {\ln |x|}{|x-1|}\sin x=\lim _{x\rightarrow 1^+}\dfrac {\ln |x|}{x-1}\sin x=\sin 1
$$
因为 $\lim _{x\rightarrow 1^-}f(x) \neq \lim _{x\rightarrow 1^+}f(x)$,所以 $x=1$ 是跳跃间断点。