题目
2.求下列各式中x的值:-|||-(1) ^2-5=dfrac (4)(9);-|||-(2) (x)^2-15=0;-|||-(3) ((x+1))^2=64;-|||-(4) ((x-3))^2-50=0.
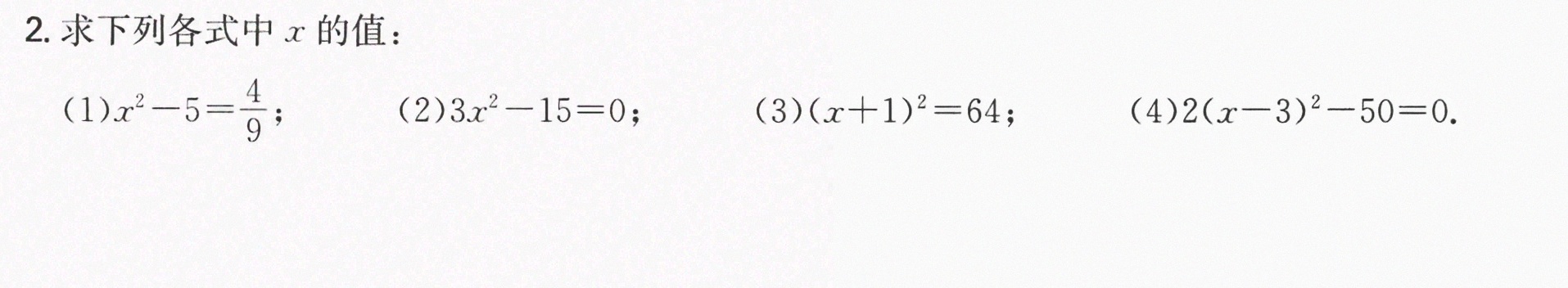
题目解答
答案
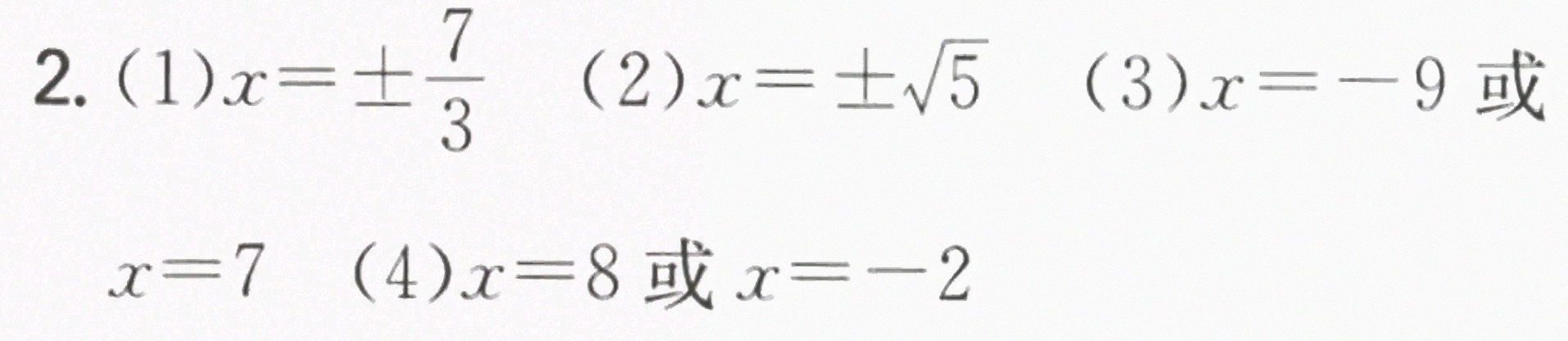
解析
步骤 1:解方程 ${x}^{2}-5=\dfrac {4}{9}$
将方程变形为 ${x}^{2}=\dfrac {4}{9}+5$,即 ${x}^{2}=\dfrac {49}{9}$,从而得到 $x=\pm \dfrac {7}{3}$。
步骤 2:解方程 $3{x}^{2}-15=0$
将方程变形为 ${x}^{2}=5$,从而得到 $x=\pm \sqrt {5}$。
步骤 3:解方程 ${(x+1)}^{2}=64$
将方程变形为 $x+1=\pm 8$,从而得到 $x=-9$ 或 $x=7$。
步骤 4:解方程 $2{(x-3)}^{2}-50=0$
将方程变形为 ${(x-3)}^{2}=25$,从而得到 $x-3=\pm 5$,从而得到 $x=8$ 或 $x=-2$。
将方程变形为 ${x}^{2}=\dfrac {4}{9}+5$,即 ${x}^{2}=\dfrac {49}{9}$,从而得到 $x=\pm \dfrac {7}{3}$。
步骤 2:解方程 $3{x}^{2}-15=0$
将方程变形为 ${x}^{2}=5$,从而得到 $x=\pm \sqrt {5}$。
步骤 3:解方程 ${(x+1)}^{2}=64$
将方程变形为 $x+1=\pm 8$,从而得到 $x=-9$ 或 $x=7$。
步骤 4:解方程 $2{(x-3)}^{2}-50=0$
将方程变形为 ${(x-3)}^{2}=25$,从而得到 $x-3=\pm 5$,从而得到 $x=8$ 或 $x=-2$。