题目
11.判断下列函数的奇偶性 。(1)(x)=x(sin )^2x;(2)(x)=x(sin )^2x;
11.判断下列函数的奇偶性 。
(1)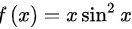 ;
;
(2)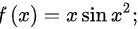 ;
;
题目解答
答案
(1)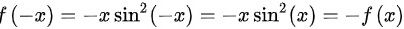
且f(0)=0,所以该函数为奇函数。
(2)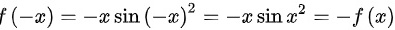
且f(0)=0,所以该函数为奇函数。
解析
考查要点:判断函数的奇偶性,需熟练掌握奇函数和偶函数的定义,并灵活运用三角函数的奇偶性进行化简。
解题核心思路:
- 奇函数定义:$f(-x) = -f(x)$;
- 偶函数定义:$f(-x) = f(x)$;
- 关键步骤:将$-x$代入函数表达式,化简后与原函数比较,判断符号关系;
- 特殊验证:若函数在$x=0$处有定义,需验证$f(0)=0$(奇函数必要条件)。
破题关键点:
- 三角函数的奇偶性:$\sin(-x) = -\sin x$,$\sin^2(-x) = \sin^2 x$;
- 平方项的符号:$(-x)^2 = x^2$,与$x$的正负无关。
第(1)题:$f(x) = x \sin^2 x$
代入$-x$计算$f(-x)$
$f(-x) = (-x) \sin^2(-x)$
利用$\sin(-x) = -\sin x$化简
$\sin^2(-x) = (-\sin x)^2 = \sin^2 x$
整体化简结果
$f(-x) = (-x) \sin^2 x = -x \sin^2 x = -f(x)$
验证$f(0)=0$
$f(0) = 0 \cdot \sin^2 0 = 0$
结论:满足奇函数定义,且$f(0)=0$,故为奇函数。
第(2)题:$f(x) = x \sin x^2$
代入$-x$计算$f(-x)$
$f(-x) = (-x) \sin((-x)^2)$
化简平方项
$(-x)^2 = x^2 \quad \Rightarrow \quad \sin((-x)^2) = \sin x^2$
整体化简结果
$f(-x) = (-x) \sin x^2 = -x \sin x^2 = -f(x)$
验证$f(0)=0$
$f(0) = 0 \cdot \sin 0^2 = 0$
结论:满足奇函数定义,且$f(0)=0$,故为奇函数。