题目
(int )_(-2)^2dfrac (x+|x|)(2+{x)^2}dx=
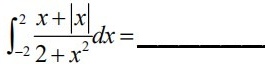
题目解答
答案
解析:
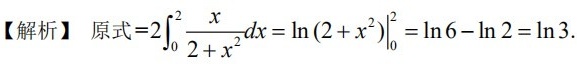
解析
步骤 1:分析被积函数
被积函数为 $\dfrac{x+|x|}{2+x^2}$,注意到 $|x|$ 在 $x \geq 0$ 时等于 $x$,在 $x < 0$ 时等于 $-x$。因此,被积函数在 $x \geq 0$ 时为 $\dfrac{2x}{2+x^2}$,在 $x < 0$ 时为 $0$。
步骤 2:分段积分
由于被积函数在 $x < 0$ 时为 $0$,因此积分可以简化为只在 $x \geq 0$ 的区间上进行。即
${\int }_{-2}^{2}\dfrac {x+|x|}{2+{x}^{2}}dx = 2{\int }_{0}^{2}\dfrac {x}{2+{x}^{2}}dx$。
步骤 3:计算积分
计算积分 $2{\int }_{0}^{2}\dfrac {x}{2+{x}^{2}}dx$,令 $u = 2 + x^2$,则 $du = 2xdx$,积分变为
$2{\int }_{0}^{2}\dfrac {x}{2+{x}^{2}}dx = {\int }_{2}^{6}\dfrac {1}{u}du = \ln u{\int }_{2}^{6} = \ln 6 - \ln 2 = \ln 3$。
被积函数为 $\dfrac{x+|x|}{2+x^2}$,注意到 $|x|$ 在 $x \geq 0$ 时等于 $x$,在 $x < 0$ 时等于 $-x$。因此,被积函数在 $x \geq 0$ 时为 $\dfrac{2x}{2+x^2}$,在 $x < 0$ 时为 $0$。
步骤 2:分段积分
由于被积函数在 $x < 0$ 时为 $0$,因此积分可以简化为只在 $x \geq 0$ 的区间上进行。即
${\int }_{-2}^{2}\dfrac {x+|x|}{2+{x}^{2}}dx = 2{\int }_{0}^{2}\dfrac {x}{2+{x}^{2}}dx$。
步骤 3:计算积分
计算积分 $2{\int }_{0}^{2}\dfrac {x}{2+{x}^{2}}dx$,令 $u = 2 + x^2$,则 $du = 2xdx$,积分变为
$2{\int }_{0}^{2}\dfrac {x}{2+{x}^{2}}dx = {\int }_{2}^{6}\dfrac {1}{u}du = \ln u{\int }_{2}^{6} = \ln 6 - \ln 2 = \ln 3$。