题目
(x)=dfrac ({x)^2-1}((x+1)(x-2))
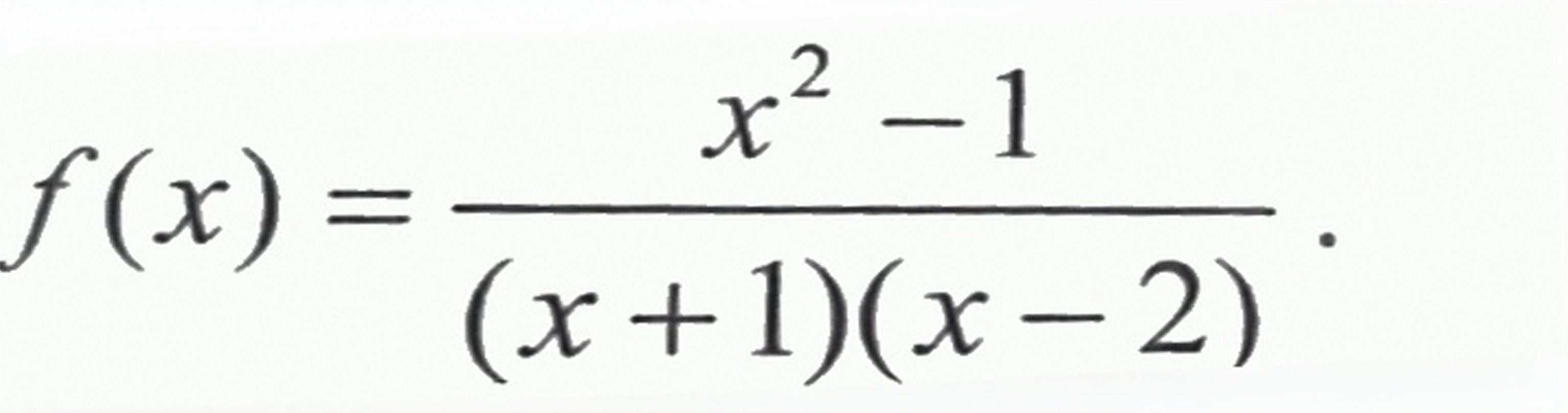
题目解答
答案
分式函数的分母不为零,
所以$x\not= -1,x\not= 2$
所以$x=-1,x=2$是间断点
$x=-1,x=2$
所以$x\not= -1,x\not= 2$
所以$x=-1,x=2$是间断点
$x=-1,x=2$
解析
步骤 1:确定分母不为零的条件
分式函数的分母不为零,因此需要确定分母$(x+1)(x-2)$不为零的条件。这意味着$x+1\not= 0$和$x-2\not= 0$。
步骤 2:求解$x+1\not= 0$和$x-2\not= 0$
解$x+1\not= 0$得到$x\not= -1$,解$x-2\not= 0$得到$x\not= 2$。因此,$x=-1$和$x=2$是函数$f(x)$的间断点。
步骤 3:总结间断点
综上所述,$x=-1$和$x=2$是函数$f(x)=\dfrac {{x}^{2}-1}{(x+1)(x-2)}$的间断点。
分式函数的分母不为零,因此需要确定分母$(x+1)(x-2)$不为零的条件。这意味着$x+1\not= 0$和$x-2\not= 0$。
步骤 2:求解$x+1\not= 0$和$x-2\not= 0$
解$x+1\not= 0$得到$x\not= -1$,解$x-2\not= 0$得到$x\not= 2$。因此,$x=-1$和$x=2$是函数$f(x)$的间断点。
步骤 3:总结间断点
综上所述,$x=-1$和$x=2$是函数$f(x)=\dfrac {{x}^{2}-1}{(x+1)(x-2)}$的间断点。