题目
[题目]解方程: (x)^2+7x+2=0
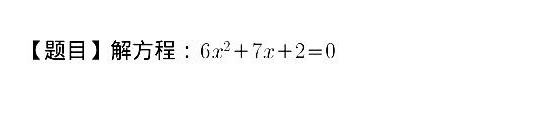
题目解答
答案

解析
考查要点:本题主要考查一元二次方程的解法,特别是因式分解法的应用。
解题思路:通过将二次三项式分解为两个一次因式的乘积,利用零乘积性质求解方程。
关键点:
- 分解二次项和常数项,寻找合适的数组合使得交叉相乘的和等于一次项系数。
- 验证分解结果是否与原方程一致。
- 分别解每个一次方程,得到最终根。
步骤1:尝试因式分解
将方程 $6x^2 + 7x + 2 = 0$ 分解为两个一次因式的乘积形式 $(ax + b)(cx + d) = 0$。
- 分解二次项:$6x^2 = 2x \cdot 3x$,因此考虑 $a=2$,$c=3$。
- 分解常数项:$2 = 1 \cdot 2$,尝试组合 $b=1$,$d=2$。
- 验证中间项:交叉相乘 $2x \cdot 2 + 3x \cdot 1 = 4x + 3x = 7x$,与原方程一致。
因此,方程可分解为:
$(2x + 1)(3x + 2) = 0$
步骤2:解一次方程
根据零乘积性质,若 $(2x + 1)(3x + 2) = 0$,则:
- $2x + 1 = 0 \Rightarrow x = -\dfrac{1}{2}$
- $3x + 2 = 0 \Rightarrow x = -\dfrac{2}{3}$
步骤3:验证解的正确性
将 $x = -\dfrac{1}{2}$ 和 $x = -\dfrac{2}{3}$ 代入原方程,均满足等式成立。