题目
int dfrac (ln x-1)({x)^2}dx=___________
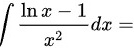 ___________
___________
题目解答
答案
分析题目所给不定积分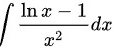 ,由凑微分法可得
,由凑微分法可得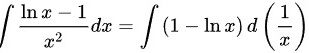
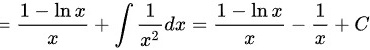
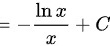 ,故本题答案为
,故本题答案为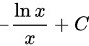
解析
步骤 1:识别积分类型
题目所给不定积分$\int \dfrac {\ln x-1}{{x}^{2}}dx$,可以使用凑微分法进行求解。
步骤 2:应用凑微分法
将积分式子变形为$\int (1-\ln x)d(\dfrac {1}{x})$,其中$d(\dfrac {1}{x})=-\dfrac {1}{{x}^{2}}dx$。
步骤 3:分部积分
根据分部积分公式$\int udv=uv-\int vdu$,令$u=1-\ln x$,$dv=-\dfrac {1}{{x}^{2}}dx$,则$du=-\dfrac {1}{x}dx$,$v=\dfrac {1}{x}$,代入公式得$\int (1-\ln x)d(\dfrac {1}{x})=(1-\ln x)\dfrac {1}{x}-\int \dfrac {1}{x}(-\dfrac {1}{x})dx$。
步骤 4:计算剩余积分
计算剩余积分$\int \dfrac {1}{{x}^{2}}dx=-\dfrac {1}{x}+C$,其中$C$为积分常数。
步骤 5:整理结果
将步骤3和步骤4的结果合并,得到$\int \dfrac {\ln x-1}{{x}^{2}}dx=\dfrac {1-\ln x}{x}-\dfrac {1}{x}+C=-\dfrac {\ln x}{x}+C$。
题目所给不定积分$\int \dfrac {\ln x-1}{{x}^{2}}dx$,可以使用凑微分法进行求解。
步骤 2:应用凑微分法
将积分式子变形为$\int (1-\ln x)d(\dfrac {1}{x})$,其中$d(\dfrac {1}{x})=-\dfrac {1}{{x}^{2}}dx$。
步骤 3:分部积分
根据分部积分公式$\int udv=uv-\int vdu$,令$u=1-\ln x$,$dv=-\dfrac {1}{{x}^{2}}dx$,则$du=-\dfrac {1}{x}dx$,$v=\dfrac {1}{x}$,代入公式得$\int (1-\ln x)d(\dfrac {1}{x})=(1-\ln x)\dfrac {1}{x}-\int \dfrac {1}{x}(-\dfrac {1}{x})dx$。
步骤 4:计算剩余积分
计算剩余积分$\int \dfrac {1}{{x}^{2}}dx=-\dfrac {1}{x}+C$,其中$C$为积分常数。
步骤 5:整理结果
将步骤3和步骤4的结果合并,得到$\int \dfrac {\ln x-1}{{x}^{2}}dx=\dfrac {1-\ln x}{x}-\dfrac {1}{x}+C=-\dfrac {\ln x}{x}+C$。