题目
求极限lim _(xarrow 0)dfrac ({x)^3+(x)^4}(x-sin x)-|||-__
求极限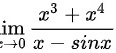
题目解答
答案
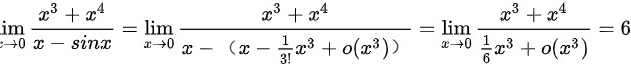
答案为6
解析
步骤 1:使用泰勒展开式
首先,我们使用泰勒展开式来近似表达式中的$\sin x$。泰勒展开式告诉我们,当$x$接近0时,$\sin x$可以近似为$x - \frac{x^3}{6} + O(x^5)$。因此,$x - \sin x$可以近似为$x - (x - \frac{x^3}{6} + O(x^5)) = \frac{x^3}{6} + O(x^5)$。
步骤 2:代入近似表达式
将$x - \sin x$的近似表达式代入原极限表达式中,得到$\lim _{x\rightarrow 0}\dfrac {{x}^{3}+{x}^{4}}{\frac{x^3}{6} + O(x^5)}$。由于$x^4$和$O(x^5)$在$x$接近0时相对于$x^3$来说是高阶无穷小,可以忽略,因此原极限可以简化为$\lim _{x\rightarrow 0}\dfrac {{x}^{3}}{\frac{x^3}{6}}$。
步骤 3:计算极限
计算简化后的极限,得到$\lim _{x\rightarrow 0}\dfrac {{x}^{3}}{\frac{x^3}{6}} = \lim _{x\rightarrow 0}6 = 6$。
首先,我们使用泰勒展开式来近似表达式中的$\sin x$。泰勒展开式告诉我们,当$x$接近0时,$\sin x$可以近似为$x - \frac{x^3}{6} + O(x^5)$。因此,$x - \sin x$可以近似为$x - (x - \frac{x^3}{6} + O(x^5)) = \frac{x^3}{6} + O(x^5)$。
步骤 2:代入近似表达式
将$x - \sin x$的近似表达式代入原极限表达式中,得到$\lim _{x\rightarrow 0}\dfrac {{x}^{3}+{x}^{4}}{\frac{x^3}{6} + O(x^5)}$。由于$x^4$和$O(x^5)$在$x$接近0时相对于$x^3$来说是高阶无穷小,可以忽略,因此原极限可以简化为$\lim _{x\rightarrow 0}\dfrac {{x}^{3}}{\frac{x^3}{6}}$。
步骤 3:计算极限
计算简化后的极限,得到$\lim _{x\rightarrow 0}\dfrac {{x}^{3}}{\frac{x^3}{6}} = \lim _{x\rightarrow 0}6 = 6$。