题目
(2) lim _(xarrow 0)dfrac ({e)^x-(e)^-x}(sin x);
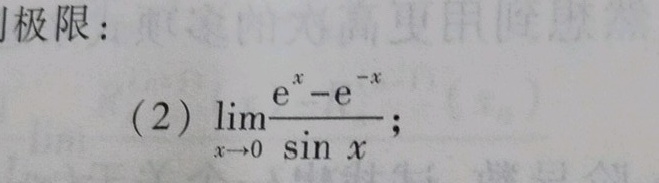
题目解答
答案
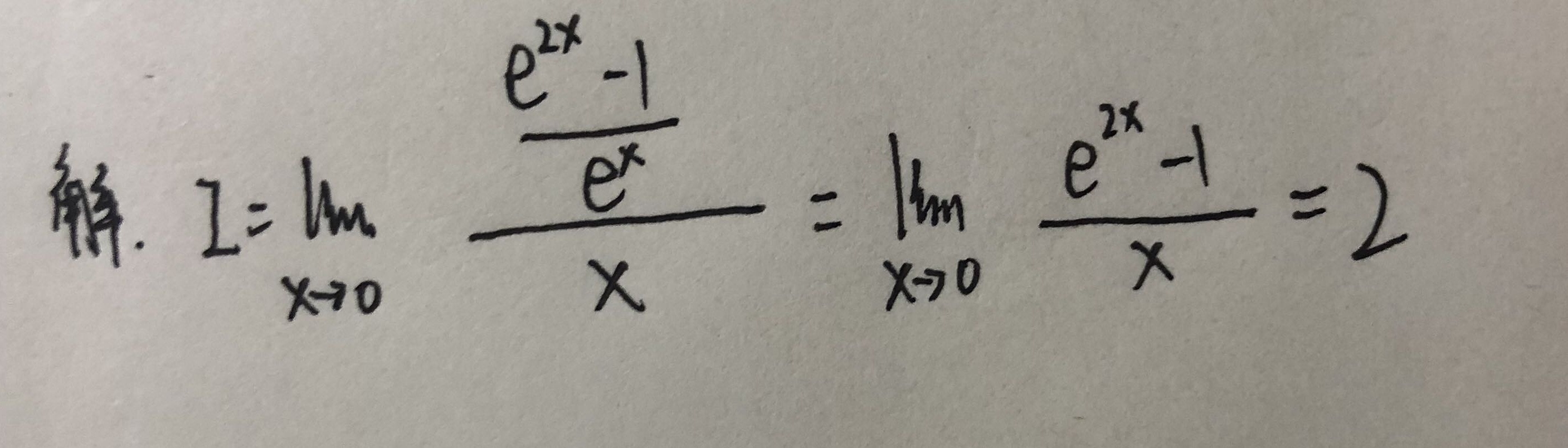
解析
步骤 1:应用洛必达法则
由于当 $x \rightarrow 0$ 时,分子和分母都趋向于0,因此可以应用洛必达法则。洛必达法则指出,如果 $\lim _{x\rightarrow a} \frac{f(x)}{g(x)}$ 形式为 $\frac{0}{0}$ 或 $\frac{\infty}{\infty}$,则 $\lim _{x\rightarrow a} \frac{f(x)}{g(x)} = \lim _{x\rightarrow a} \frac{f'(x)}{g'(x)}$,只要后者存在或为无穷大。
步骤 2:求导
对分子和分母分别求导,得到 $\lim _{x\rightarrow 0} \frac{e^x + e^{-x}}{\cos x}$。
步骤 3:计算极限
将 $x = 0$ 代入上述表达式,得到 $\frac{e^0 + e^{-0}}{\cos 0} = \frac{1 + 1}{1} = 2$。
由于当 $x \rightarrow 0$ 时,分子和分母都趋向于0,因此可以应用洛必达法则。洛必达法则指出,如果 $\lim _{x\rightarrow a} \frac{f(x)}{g(x)}$ 形式为 $\frac{0}{0}$ 或 $\frac{\infty}{\infty}$,则 $\lim _{x\rightarrow a} \frac{f(x)}{g(x)} = \lim _{x\rightarrow a} \frac{f'(x)}{g'(x)}$,只要后者存在或为无穷大。
步骤 2:求导
对分子和分母分别求导,得到 $\lim _{x\rightarrow 0} \frac{e^x + e^{-x}}{\cos x}$。
步骤 3:计算极限
将 $x = 0$ 代入上述表达式,得到 $\frac{e^0 + e^{-0}}{\cos 0} = \frac{1 + 1}{1} = 2$。