题目
(2)若 lim _(xarrow infty )((1+dfrac {k)(x))}^-3x=(e)^-1 ,则 k= __
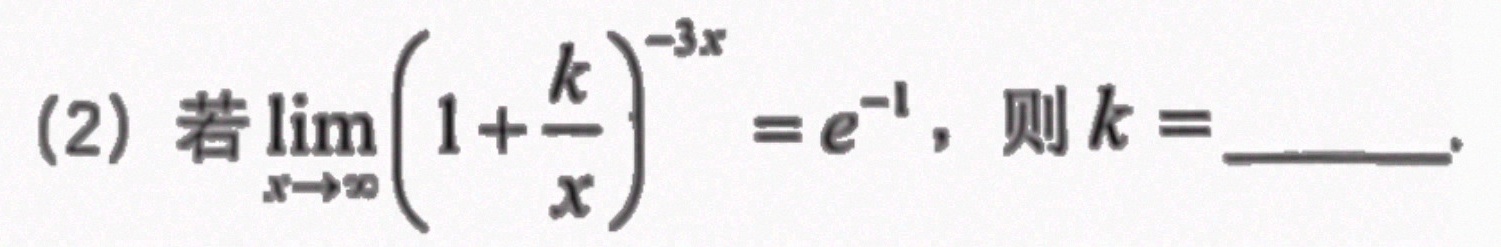
题目解答
答案

解析
步骤 1:将给定的极限表达式转换为自然对数形式
给定的极限表达式为 $\lim _{x\rightarrow \infty }{(1+\dfrac {k}{x})}^{-3x}={e}^{-1}$。首先,我们可以通过对两边取自然对数来简化问题。即,$\ln(\lim _{x\rightarrow \infty }{(1+\dfrac {k}{x})}^{-3x})=\ln({e}^{-1})$。由于自然对数和指数函数是互为逆运算,我们有 $\lim _{x\rightarrow \infty }(-3x\ln(1+\dfrac {k}{x}))=-1$。
步骤 2:利用洛必达法则求解
接下来,我们注意到当 $x\rightarrow \infty$ 时,$-3x\ln(1+\dfrac {k}{x})$ 形式为 $\infty \cdot 0$,这是一个不定型。为了求解这个极限,我们可以使用洛必达法则。首先,将表达式重写为 $\lim _{x\rightarrow \infty }\dfrac {\ln(1+\dfrac {k}{x})}{\dfrac {1}{-3x}}$,这样就转换成了 $\dfrac {0}{0}$ 的形式,适合应用洛必达法则。应用洛必达法则,我们对分子和分母分别求导,得到 $\lim _{x\rightarrow \infty }\dfrac {\dfrac {1}{1+\dfrac {k}{x}}\cdot \dfrac {-k}{x^2}}{\dfrac {1}{3x^2}}$。简化后得到 $\lim _{x\rightarrow \infty }\dfrac {-3k}{1+\dfrac {k}{x}}$。当 $x\rightarrow \infty$ 时,$\dfrac {k}{x}\rightarrow 0$,因此极限值为 $-3k$。
步骤 3:求解 k 的值
根据步骤 2 的结果,我们有 $-3k=-1$。解这个方程,得到 $k=\dfrac {1}{3}$。
给定的极限表达式为 $\lim _{x\rightarrow \infty }{(1+\dfrac {k}{x})}^{-3x}={e}^{-1}$。首先,我们可以通过对两边取自然对数来简化问题。即,$\ln(\lim _{x\rightarrow \infty }{(1+\dfrac {k}{x})}^{-3x})=\ln({e}^{-1})$。由于自然对数和指数函数是互为逆运算,我们有 $\lim _{x\rightarrow \infty }(-3x\ln(1+\dfrac {k}{x}))=-1$。
步骤 2:利用洛必达法则求解
接下来,我们注意到当 $x\rightarrow \infty$ 时,$-3x\ln(1+\dfrac {k}{x})$ 形式为 $\infty \cdot 0$,这是一个不定型。为了求解这个极限,我们可以使用洛必达法则。首先,将表达式重写为 $\lim _{x\rightarrow \infty }\dfrac {\ln(1+\dfrac {k}{x})}{\dfrac {1}{-3x}}$,这样就转换成了 $\dfrac {0}{0}$ 的形式,适合应用洛必达法则。应用洛必达法则,我们对分子和分母分别求导,得到 $\lim _{x\rightarrow \infty }\dfrac {\dfrac {1}{1+\dfrac {k}{x}}\cdot \dfrac {-k}{x^2}}{\dfrac {1}{3x^2}}$。简化后得到 $\lim _{x\rightarrow \infty }\dfrac {-3k}{1+\dfrac {k}{x}}$。当 $x\rightarrow \infty$ 时,$\dfrac {k}{x}\rightarrow 0$,因此极限值为 $-3k$。
步骤 3:求解 k 的值
根据步骤 2 的结果,我们有 $-3k=-1$。解这个方程,得到 $k=\dfrac {1}{3}$。