题目
4.曲线 =xln (2+dfrac (1)(x)) 的渐近线为_
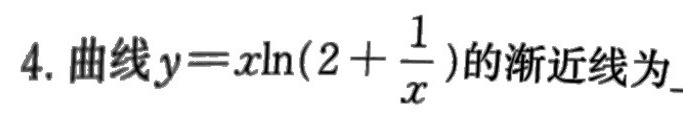
题目解答
答案

解析
考查要点:本题主要考查曲线渐近线的求解,包括垂直渐近线、水平渐近线和斜渐近线的判断方法。
解题核心思路:
- 垂直渐近线:寻找函数中使分母趋近于0或对数函数内部趋近于0的点,分析函数值是否趋向无穷。
- 水平渐近线:计算当$x \to \pm\infty$时函数的极限,若极限为常数则存在水平渐近线。
- 斜渐近线:当水平渐近线不存在时,计算斜率$a = \lim_{x \to \infty} \frac{y}{x}$,再求截距$b = \lim_{x \to \infty} (y - a x)$。
破题关键点:
- 垂直渐近线的关键是找到使对数函数内部$2 + \frac{1}{x} \to 0$的$x$值。
- 斜渐近线需通过泰勒展开或等价无穷小替换简化表达式,提取一次项和常数项。
垂直渐近线
当$x \to -\frac{1}{2}$时,$\frac{1}{x} \to -2$,因此$2 + \frac{1}{x} \to 0^+$,此时$\ln\left(2 + \frac{1}{x}\right) \to -\infty$。由于$x \to -\frac{1}{2}$为有限值,函数值$y = x \ln\left(2 + \frac{1}{x}\right) \to +\infty$,故垂直渐近线为$x = -\frac{1}{2}$。
水平渐近线
- 当$x \to +\infty$时:$\frac{1}{x} \to 0$,$\ln\left(2 + \frac{1}{x}\right) \to \ln 2$,此时$y \approx x \ln 2 \to +\infty$,无水平渐近线。
- 当$x \to -\infty$时:$\frac{1}{x} \to 0$,同理$y \approx x \ln 2 \to -\infty$,无水平渐近线。
斜渐近线
当$x \to +\infty$时,对$\ln\left(2 + \frac{1}{x}\right)$进行泰勒展开:
$\ln\left(2 + \frac{1}{x}\right) = \ln 2 + \frac{1}{2x} - \frac{1}{8x^2} + \cdots$
代入原函数:
$y = x \left( \ln 2 + \frac{1}{2x} - \frac{1}{8x^2} + \cdots \right) = x \ln 2 + \frac{1}{2} - \frac{1}{8x} + \cdots$
当$x \to +\infty$时,高阶小项可忽略,故斜渐近线为$y = x \ln 2 + \frac{1}{2}$。