题目
lim _(xarrow 0)dfrac ({x)^2sin dfrac (1)(x)}(tan x)=A.0B.1C.lim _(xarrow 0)dfrac ({x)^2sin dfrac (1)(x)}(tan x)=D.-1
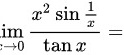
A.0
B.1
C.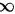
D.-1
题目解答
答案
解：根据题意可得极限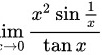
，
由等价无穷小的替换，可得
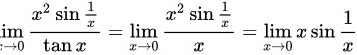
∵当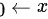
时，-1≤sin
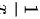≤1,
∴
=0.
故答案选A.
解析
步骤 1：应用等价无穷小替换
在极限计算中，当$x\rightarrow 0$时，$\tan x$可以被$x$替换，因为$\tan x$和$x$是等价无穷小。因此，原极限可以简化为$\lim _{x\rightarrow 0}\dfrac {{x}^{2}\sin \dfrac {1}{x}}{x}$。
步骤 2：简化表达式
将$\tan x$替换为$x$后，原极限变为$\lim _{x\rightarrow 0}x\sin \dfrac {1}{x}$。这一步简化了极限的计算，使得我们能够更直接地分析$x\rightarrow 0$时的极限行为。
步骤 3：分析极限行为
当$x\rightarrow 0$时，$\sin \dfrac {1}{x}$的值在-1和1之间波动，但$x$的值趋向于0。因此，$x\sin \dfrac {1}{x}$的值趋向于0，因为$x$的趋向于0的效应超过了$\sin \dfrac {1}{x}$的波动效应。
在极限计算中，当$x\rightarrow 0$时，$\tan x$可以被$x$替换，因为$\tan x$和$x$是等价无穷小。因此，原极限可以简化为$\lim _{x\rightarrow 0}\dfrac {{x}^{2}\sin \dfrac {1}{x}}{x}$。
步骤 2：简化表达式
将$\tan x$替换为$x$后，原极限变为$\lim _{x\rightarrow 0}x\sin \dfrac {1}{x}$。这一步简化了极限的计算，使得我们能够更直接地分析$x\rightarrow 0$时的极限行为。
步骤 3：分析极限行为
当$x\rightarrow 0$时，$\sin \dfrac {1}{x}$的值在-1和1之间波动，但$x$的值趋向于0。因此，$x\sin \dfrac {1}{x}$的值趋向于0，因为$x$的趋向于0的效应超过了$\sin \dfrac {1}{x}$的波动效应。