题目

求极限lim _(xarrow 2)(dfrac (1)({x)^2-3x+2})-(dfrac (1)(x-2))-|||-__

求极限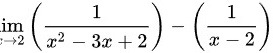 $\lim_{x\rightarrow2}\left(\frac{1}{x^2-3x+2}\right)-\left(\frac{1}{x-2}\right)$

题目解答

答案

由题可得：

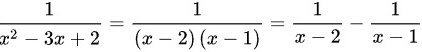
$\frac{1}{x^2-3x+2}=\frac{1}{\left(x-2\right)\left(x-1\right)}=\frac{1}{x-2}-\frac{1}{x-1}$

所以有：

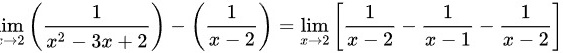
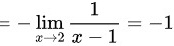
$\lim_{x\rightarrow2}\left(\frac{1}{x^2-3x+2}\right)-\left(\frac{1}{x-2}\right)=\lim_{x\rightarrow2}\left[\frac{1}{x-2}-\frac{1}{x-1}-\frac{1}{x-2}\right]$

$=-\lim_{x\rightarrow2}\frac{1}{x-1}=-1$

综上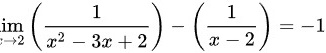， $\lim_{x\rightarrow2}\left(\frac{1}{x^2-3x+2}\right)-\left(\frac{1}{x-2}\right)=-1$

解析

步骤 1：分解分母
首先，我们注意到分母${x}^{2}-3x+2$可以分解为$(x-2)(x-1)$，因为$(x-2)(x-1)={x}^{2}-3x+2$。
步骤 2：化简表达式
将原表达式$\dfrac {1}{{x}^{2}-3x+2}-(\dfrac {1}{x-2})$中的分母${x}^{2}-3x+2$替换为$(x-2)(x-1)$，得到$\dfrac {1}{(x-2)(x-1)}-(\dfrac {1}{x-2})$。
步骤 3：合并同类项
将$\dfrac {1}{(x-2)(x-1)}$写为$\dfrac {1}{x-2}-\dfrac {1}{x-1}$，然后与$-\dfrac {1}{x-2}$合并，得到$-\dfrac {1}{x-1}$。
步骤 4：求极限
当$x\rightarrow 2$时，$-\dfrac {1}{x-1}$的极限为$-\dfrac {1}{2-1}=-1$。