题目
在Rt△ABC中,∠ACB=90°,AC=BC,∠CAB=∠CBA=45°,D为BC上一点,连接AD,过点C作CE⊥AD于点E.()-|||-E-|||-B-|||-图1 F-|||-C-|||-D-|||-E-|||-A.-|||-M B-|||-图2(1)如图1,过点B作BF⊥BC交CE的延长线于点F,求证:△ACD≌△CBF;(2)如图2,若D为BC的中点,CE的延长线交AB于点M,连接DM,求证:∠BDM=∠ADC;(3)在(2)的条件下,若AE=4,CE=2,直接写出CM的长.
在Rt△ABC中,∠ACB=90°,AC=BC,∠CAB=∠CBA=45°,D为BC上一点,连接AD,过点C作CE⊥AD于点E.
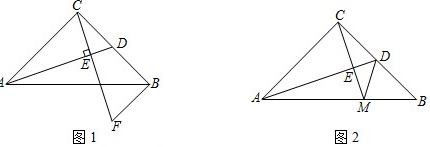
(1)如图1,过点B作BF⊥BC交CE的延长线于点F,求证:△ACD≌△CBF;
(2)如图2,若D为BC的中点,CE的延长线交AB于点M,连接DM,求证:∠BDM=∠ADC;
(3)在(2)的条件下,若AE=4,CE=2,直接写出CM的长.
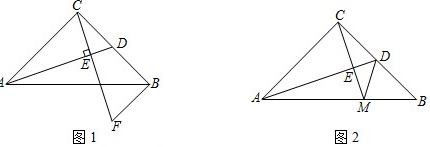
(1)如图1,过点B作BF⊥BC交CE的延长线于点F,求证:△ACD≌△CBF;
(2)如图2,若D为BC的中点,CE的延长线交AB于点M,连接DM,求证:∠BDM=∠ADC;
(3)在(2)的条件下,若AE=4,CE=2,直接写出CM的长.
题目解答
答案
(1)证明:∵BF⊥BC,CE⊥AD,
∴∠AEC=∠CBF=∠ACB=90°,
∴∠CAD+∠ACE=∠BCF+∠ACE=90°,
∴∠CAD=∠BCF,
又∵AC=BC,
∴△ACD≌△CBF(ASA);
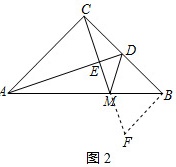 (2)证明:过点B作BF⊥BC交CE的延长线于点F,如图2所示:
(2)证明:过点B作BF⊥BC交CE的延长线于点F,如图2所示:
由(1)得:△ACD≌△CBF,
∴∠ADC=∠F,CD=BF,
∵D为BC的中点,
∴CD=BD,
∴BD=BF,
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∵∠CBF=90°,
∴∠FBM=90°-45°=45°,
∴∠DBM=∠FBM,
又∵BM=BM,
∴△BDM≌△BFM(SAS),
∴∠BDM=∠F,
∴∠BDM=∠ADC;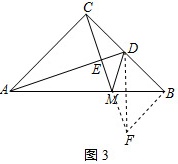
(3)解:连接DF,如图3所示:
∵CE⊥AD,AE=4,CE=2,
∴BC=AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
由(2)得:BD=BF,CD=BD=$\frac{1}{2}$BC=$\sqrt{5}$,△BDM≌△BFM,
∴DM=FM,AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{(2\sqrt{5})^{2}+(\sqrt{5})^{2}}$=5,
∴DE=AD-AE=1,
∵∠DBF=90°,
∴△BDF是等腰直角三角形,
∴DF=$\sqrt{2}$BD=$\sqrt{10}$,
∴EF=$\sqrt{D{F}^{2}-D{E}^{2}}$=$\sqrt{(\sqrt{10})^{2}-{1}^{2}}$=3,
设DM=FM=x,则EM=3-x,
在Rt△DEM中,由勾股定理得:12+(3-x)2=x2,
解得:x=$\frac{5}{3}$,
∴EM=3-$\frac{5}{3}$=$\frac{4}{3}$,
∴CM=CE+EM=2+$\frac{4}{3}$=$\frac{10}{3}$.
∴∠AEC=∠CBF=∠ACB=90°,
∴∠CAD+∠ACE=∠BCF+∠ACE=90°,
∴∠CAD=∠BCF,
又∵AC=BC,
∴△ACD≌△CBF(ASA);
 (2)证明:过点B作BF⊥BC交CE的延长线于点F,如图2所示:
(2)证明:过点B作BF⊥BC交CE的延长线于点F,如图2所示:由(1)得:△ACD≌△CBF,
∴∠ADC=∠F,CD=BF,
∵D为BC的中点,
∴CD=BD,
∴BD=BF,
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∵∠CBF=90°,
∴∠FBM=90°-45°=45°,
∴∠DBM=∠FBM,
又∵BM=BM,
∴△BDM≌△BFM(SAS),
∴∠BDM=∠F,
∴∠BDM=∠ADC;

(3)解:连接DF,如图3所示:
∵CE⊥AD,AE=4,CE=2,
∴BC=AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
由(2)得:BD=BF,CD=BD=$\frac{1}{2}$BC=$\sqrt{5}$,△BDM≌△BFM,
∴DM=FM,AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{(2\sqrt{5})^{2}+(\sqrt{5})^{2}}$=5,
∴DE=AD-AE=1,
∵∠DBF=90°,
∴△BDF是等腰直角三角形,
∴DF=$\sqrt{2}$BD=$\sqrt{10}$,
∴EF=$\sqrt{D{F}^{2}-D{E}^{2}}$=$\sqrt{(\sqrt{10})^{2}-{1}^{2}}$=3,
设DM=FM=x,则EM=3-x,
在Rt△DEM中,由勾股定理得:12+(3-x)2=x2,
解得:x=$\frac{5}{3}$,
∴EM=3-$\frac{5}{3}$=$\frac{4}{3}$,
∴CM=CE+EM=2+$\frac{4}{3}$=$\frac{10}{3}$.
解析
步骤 1:证明△ACD≌△CBF
根据已知条件,通过角边角(ASA)定理证明两个三角形全等。
步骤 2:证明∠BDM=∠ADC
通过构造辅助线,利用边角边(SAS)定理证明两个三角形全等,从而证明角相等。
步骤 3:计算CM的长度
通过勾股定理和等腰直角三角形的性质,计算出CM的长度。
根据已知条件,通过角边角(ASA)定理证明两个三角形全等。
步骤 2:证明∠BDM=∠ADC
通过构造辅助线,利用边角边(SAS)定理证明两个三角形全等,从而证明角相等。
步骤 3:计算CM的长度
通过勾股定理和等腰直角三角形的性质,计算出CM的长度。