题目
求极限lim _(narrow infty )(dfrac (n)({n)^2+1}+dfrac (n)({n)^2+2}+... +dfrac (n)({n)^2+n})
求极限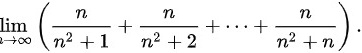
题目解答
答案
由题意得,
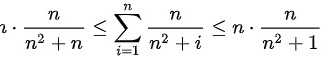
所以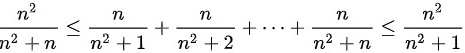 ,因为
,因为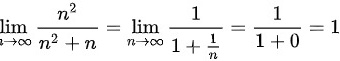
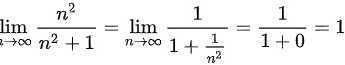 ,故由夹逼准则可得,
,故由夹逼准则可得,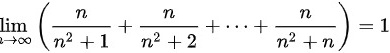
故答案为 .
.
解析
步骤 1:确定极限表达式
给定极限表达式为$\lim _{n\rightarrow \infty }(\dfrac {n}{{n}^{2}+1}+\dfrac {n}{{n}^{2}+2}+\cdots +\dfrac {n}{{n}^{2}+n})$,这是一个求和形式的极限问题,其中每一项都是分式形式,分母为$n^2$加上一个从1到n的整数。
步骤 2:应用夹逼准则
为了应用夹逼准则,我们需要找到一个下界和一个上界,使得这两个界在$n\rightarrow \infty$时都收敛到同一个值。对于给定的求和表达式,我们可以观察到每一项$\dfrac{n}{{n}^{2}+i}$(其中$i$从1到$n$)都满足$\dfrac{n}{{n}^{2}+n}\leqslant \dfrac{n}{{n}^{2}+i}\leqslant \dfrac{n}{{n}^{2}+1}$。因此,整个求和表达式的下界为$\dfrac{n}{{n}^{2}+n}$乘以项数$n$,上界为$\dfrac{n}{{n}^{2}+1}$乘以项数$n$。
步骤 3:计算上下界极限
计算下界极限:$\lim _{n\rightarrow \infty }\dfrac {{n}^{2}}{{n}^{2}+n}=\lim _{n\rightarrow \infty }\dfrac {1}{1+\dfrac {1}{n}}=\dfrac {1}{1+0}=1$。
计算上界极限:$\lim _{n\rightarrow \infty }\dfrac {{n}^{2}}{{n}^{2}+1}=\lim _{n\rightarrow \infty }\dfrac {1}{1+\dfrac {1}{{n}^{2}}}=\dfrac {1}{1+0}=1$。
由于上下界极限都等于1,根据夹逼准则,原极限也等于1。
给定极限表达式为$\lim _{n\rightarrow \infty }(\dfrac {n}{{n}^{2}+1}+\dfrac {n}{{n}^{2}+2}+\cdots +\dfrac {n}{{n}^{2}+n})$,这是一个求和形式的极限问题,其中每一项都是分式形式,分母为$n^2$加上一个从1到n的整数。
步骤 2:应用夹逼准则
为了应用夹逼准则,我们需要找到一个下界和一个上界,使得这两个界在$n\rightarrow \infty$时都收敛到同一个值。对于给定的求和表达式,我们可以观察到每一项$\dfrac{n}{{n}^{2}+i}$(其中$i$从1到$n$)都满足$\dfrac{n}{{n}^{2}+n}\leqslant \dfrac{n}{{n}^{2}+i}\leqslant \dfrac{n}{{n}^{2}+1}$。因此,整个求和表达式的下界为$\dfrac{n}{{n}^{2}+n}$乘以项数$n$,上界为$\dfrac{n}{{n}^{2}+1}$乘以项数$n$。
步骤 3:计算上下界极限
计算下界极限:$\lim _{n\rightarrow \infty }\dfrac {{n}^{2}}{{n}^{2}+n}=\lim _{n\rightarrow \infty }\dfrac {1}{1+\dfrac {1}{n}}=\dfrac {1}{1+0}=1$。
计算上界极限:$\lim _{n\rightarrow \infty }\dfrac {{n}^{2}}{{n}^{2}+1}=\lim _{n\rightarrow \infty }\dfrac {1}{1+\dfrac {1}{{n}^{2}}}=\dfrac {1}{1+0}=1$。
由于上下界极限都等于1,根据夹逼准则,原极限也等于1。