题目
.求极限 lim _(xarrow infty )dfrac (arctan x)(x).
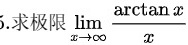 .
.
题目解答
答案
解:
解析
步骤 1:确定函数的性质
当 $x \rightarrow \infty$ 时,$\dfrac{1}{x}$ 是无穷小量,而 $\arctan x$ 是有界函数,因为 $\arctan x$ 的值域为 $(-\frac{\pi}{2}, \frac{\pi}{2})$。
步骤 2:应用无穷小量与有界函数的乘积性质
根据无穷小量与有界函数的乘积性质,当 $x \rightarrow \infty$ 时,$\dfrac{1}{x} \cdot \arctan x$ 是无穷小量。
步骤 3:计算极限
根据上述性质,可以得出 $\lim _{x\rightarrow \infty }\dfrac {\arctan x}{x} = 0$。
当 $x \rightarrow \infty$ 时,$\dfrac{1}{x}$ 是无穷小量,而 $\arctan x$ 是有界函数,因为 $\arctan x$ 的值域为 $(-\frac{\pi}{2}, \frac{\pi}{2})$。
步骤 2:应用无穷小量与有界函数的乘积性质
根据无穷小量与有界函数的乘积性质,当 $x \rightarrow \infty$ 时,$\dfrac{1}{x} \cdot \arctan x$ 是无穷小量。
步骤 3:计算极限
根据上述性质,可以得出 $\lim _{x\rightarrow \infty }\dfrac {\arctan x}{x} = 0$。