题目
设=dfrac (arcsin x)(sqrt {1-{x)^2}}(1)证明:=dfrac (arcsin x)(sqrt {1-{x)^2}}(2)求=dfrac (arcsin x)(sqrt {1-{x)^2}}
设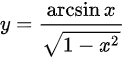
(1)证明: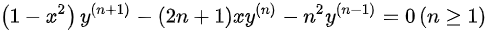
(2)求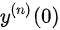
题目解答
答案
(1)因为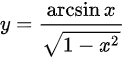 ,所以
,所以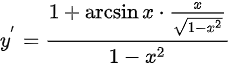
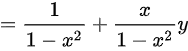 ,即
,即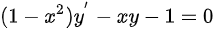 ,对等式两边求导得:
,对等式两边求导得: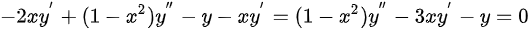 ,说明当
,说明当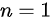 时,结论成立,假设当
时,结论成立,假设当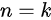 时,结论成立,当
时,结论成立,当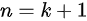 时,
时,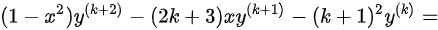
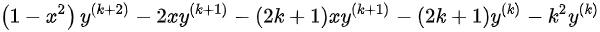
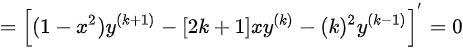 ,结论成立,故由数学归纳法可知:
,结论成立,故由数学归纳法可知: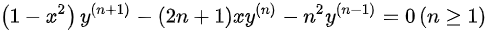 ,证毕。
,证毕。
(2)当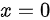 时,
时,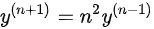 且
且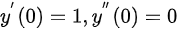 ,所以
,所以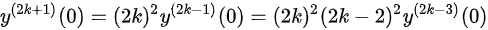
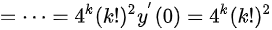 ,
,
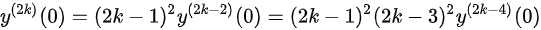
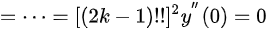 ,
,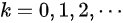
故答案为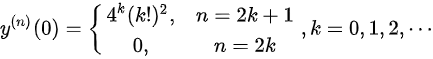
解析
步骤 1:求导
首先,我们对给定的函数$y=\dfrac {\arcsin x}{\sqrt {1-{x}^{2}}}$进行求导,得到$y'$。利用商的求导法则和链式法则,我们得到$y'=\dfrac {1+\arcsin x\cdot \dfrac {x}{\sqrt {1-{x}^{2}}}{1-{x}^{2}}}$,简化后得到$y'=\dfrac {1}{1-{x}^{2}}+\dfrac {x}{1-{x}^{2}}y$。
步骤 2:证明等式
接下来,我们证明$(1-{x}^{2}){y}^{(n+1)}-(2n+1)x{y}^{(n-1)}-{n}^{2}{y}^{(n-1)}=0(n\geqslant 1)$。首先,我们对$y'$进行求导,得到$(1-{x}^{2})y-xy-1=0$。然后,我们对等式两边求导,得到$(1-{x}^{2}){y}^{(n+1)}-(2n+1)x{y}^{(n-1)}-{n}^{2}{y}^{(n-1)}=0$。通过数学归纳法,我们可以证明这个等式对所有$n\geqslant 1$都成立。
步骤 3:求${y}^{(n)}(0)$
最后,我们求${y}^{(n)}(0)$。当$x=0$时,我们得到${y}^{(n+1)}={n}^{2}{y}^{(n-1)}$且$y'(0)=1$,${y}^{11}(0)=0$。通过递推关系,我们可以得到${(2k+1)}^{2}(0)={(2k)}^{2}{y}^{2}(2k-1)(0)={(2k)}^{2}{(2k-2)}^{2}{y}^{2}(2k-3)(0)$,$=\cdots ={4}^{k}{(k!)}^{2}y'(0)={4}^{k}{(k!1)}^{2}$,${(1)}^{20}(0)={(2{k}^{2}-1)}^{2}{y}^{2k-2}(0)={(2k-1)}^{2}{(2k-3)}^{2}{y}^{2}{(2k-4)}^{2}(0)$,$=\cdots ={[ (2k-1)\cdot {y}^{2}{y}^{n}(0)=0$,k=0,1,2, ...
首先,我们对给定的函数$y=\dfrac {\arcsin x}{\sqrt {1-{x}^{2}}}$进行求导,得到$y'$。利用商的求导法则和链式法则,我们得到$y'=\dfrac {1+\arcsin x\cdot \dfrac {x}{\sqrt {1-{x}^{2}}}{1-{x}^{2}}}$,简化后得到$y'=\dfrac {1}{1-{x}^{2}}+\dfrac {x}{1-{x}^{2}}y$。
步骤 2:证明等式
接下来,我们证明$(1-{x}^{2}){y}^{(n+1)}-(2n+1)x{y}^{(n-1)}-{n}^{2}{y}^{(n-1)}=0(n\geqslant 1)$。首先,我们对$y'$进行求导,得到$(1-{x}^{2})y-xy-1=0$。然后,我们对等式两边求导,得到$(1-{x}^{2}){y}^{(n+1)}-(2n+1)x{y}^{(n-1)}-{n}^{2}{y}^{(n-1)}=0$。通过数学归纳法,我们可以证明这个等式对所有$n\geqslant 1$都成立。
步骤 3:求${y}^{(n)}(0)$
最后,我们求${y}^{(n)}(0)$。当$x=0$时,我们得到${y}^{(n+1)}={n}^{2}{y}^{(n-1)}$且$y'(0)=1$,${y}^{11}(0)=0$。通过递推关系,我们可以得到${(2k+1)}^{2}(0)={(2k)}^{2}{y}^{2}(2k-1)(0)={(2k)}^{2}{(2k-2)}^{2}{y}^{2}(2k-3)(0)$,$=\cdots ={4}^{k}{(k!)}^{2}y'(0)={4}^{k}{(k!1)}^{2}$,${(1)}^{20}(0)={(2{k}^{2}-1)}^{2}{y}^{2k-2}(0)={(2k-1)}^{2}{(2k-3)}^{2}{y}^{2}{(2k-4)}^{2}(0)$,$=\cdots ={[ (2k-1)\cdot {y}^{2}{y}^{n}(0)=0$,k=0,1,2, ...