题目
3.已知 =sqrt (n+1)-sqrt (n) . =sqrt (n+2)-sqrt (n+1) , gt 0 ,试比较-|||-a,b的大小.
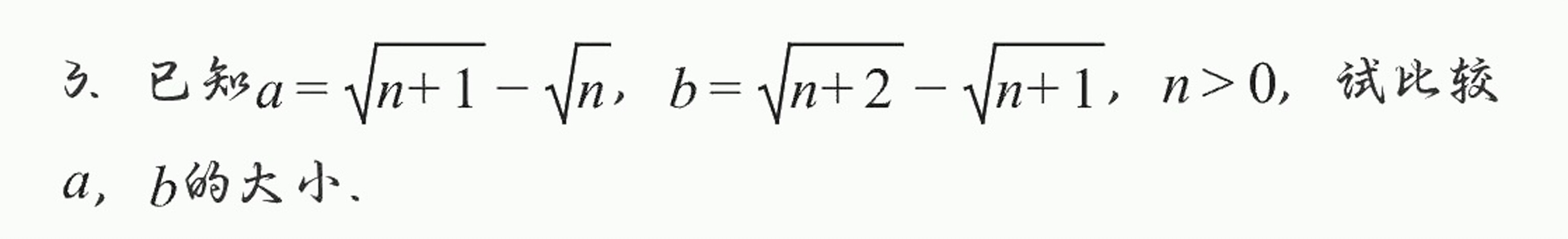
题目解答
答案
本题考查了二次根式的性质和二次根式的加减,先将a、b分母有理化,再比较分母的大小,即可得出a、b的大小。
$\because a=\dfrac {1} {\sqrt {n+1}+\sqrt {n}}$,$b=\dfrac {1} {\sqrt {n+2}+\sqrt {n+1}}$,
$\therefore \sqrt {n+1}+\sqrt {n}\lt \sqrt {n+2}+\sqrt {n+1}$,
$\therefore \dfrac {1} {\sqrt {n+1}+\sqrt {n}}\gt \dfrac {1} {\sqrt {n+2}+\sqrt {n+1}}$,
$\therefore a\gt b$.
$\because a=\dfrac {1} {\sqrt {n+1}+\sqrt {n}}$,$b=\dfrac {1} {\sqrt {n+2}+\sqrt {n+1}}$,
$\therefore \sqrt {n+1}+\sqrt {n}\lt \sqrt {n+2}+\sqrt {n+1}$,
$\therefore \dfrac {1} {\sqrt {n+1}+\sqrt {n}}\gt \dfrac {1} {\sqrt {n+2}+\sqrt {n+1}}$,
$\therefore a\gt b$.
解析
考查要点:本题主要考查二次根式的分母有理化及分数大小的比较方法。
解题思路:通过分母有理化将$a$和$b$转化为倒数形式,比较分母的大小关系,从而判断$a$和$b$的大小。
关键点:
- 分母有理化:利用平方差公式将$a$和$b$的表达式变形,使分母变为有理数。
- 分数比较:分子相同的情况下,分母越大,分数值越小。
步骤1:对$a$进行分母有理化
$a = \sqrt{n+1} - \sqrt{n} = \frac{(\sqrt{n+1} - \sqrt{n})(\sqrt{n+1} + \sqrt{n})}{\sqrt{n+1} + \sqrt{n}} = \frac{1}{\sqrt{n+1} + \sqrt{n}}.$
步骤2:对$b$进行分母有理化
$b = \sqrt{n+2} - \sqrt{n+1} = \frac{(\sqrt{n+2} - \sqrt{n+1})(\sqrt{n+2} + \sqrt{n+1})}{\sqrt{n+2} + \sqrt{n+1}} = \frac{1}{\sqrt{n+2} + \sqrt{n+1}}.$
步骤3:比较分母大小
分母分别为$\sqrt{n+1} + \sqrt{n}$和$\sqrt{n+2} + \sqrt{n+1}$。
由于$n > 0$,显然$\sqrt{n+2} > \sqrt{n}$,因此:
$\sqrt{n+1} + \sqrt{n} < \sqrt{n+2} + \sqrt{n+1}.$
步骤4:比较$a$和$b$的大小
分子均为1,分母越大分数值越小,因此:
$\frac{1}{\sqrt{n+1} + \sqrt{n}} > \frac{1}{\sqrt{n+2} + \sqrt{n+1}} \implies a > b.$