题目
求下列函数的极限lim _(xarrow infty )dfrac ({(2x-1))^10((7x+2))^20}(5{x)^30}
求下列函数的极限
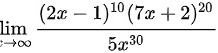
题目解答
答案
函数
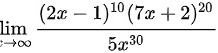，分子是两个多项式的乘积：
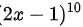和
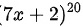，可以通过分析最高次项来计算极限。
分子的最高次项为：
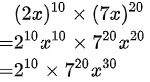
分母为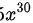
当
时，只考虑分子分母的最高次项。
则原式可化为：
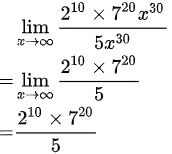
答案为：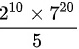
解析
步骤 1：分析分子的最高次项
分子是两个多项式的乘积：${(2x-1)}^{10}$和${(7x+2)}^{20}$。当$x$趋向于无穷大时，只考虑分子分母的最高次项。对于${(2x-1)}^{10}$，最高次项是${(2x)}^{10}$，对于${(7x+2)}^{20}$，最高次项是${(7x)}^{20}$。因此，分子的最高次项为${(2x)}^{10}{(7x)}^{20}$。
步骤 2：计算分子的最高次项
分子的最高次项为${(2x)}^{10}{(7x)}^{20} = {2}^{10}{x}^{10}{7}^{20}{x}^{20} = {2}^{10}{7}^{20}{x}^{30}$。
步骤 3：计算极限
分母为$5{x}^{30}$。当$x$趋向于无穷大时，只考虑分子分母的最高次项。因此，原式可化为$\lim _{x\rightarrow \infty }\dfrac {{2}^{10}{7}^{20}{x}^{30}}{5{x}^{30}}$。由于${x}^{30}$在分子和分母中相互抵消，极限值为$\dfrac {{2}^{10}{7}^{20}}{5}$。
分子是两个多项式的乘积：${(2x-1)}^{10}$和${(7x+2)}^{20}$。当$x$趋向于无穷大时，只考虑分子分母的最高次项。对于${(2x-1)}^{10}$，最高次项是${(2x)}^{10}$，对于${(7x+2)}^{20}$，最高次项是${(7x)}^{20}$。因此，分子的最高次项为${(2x)}^{10}{(7x)}^{20}$。
步骤 2：计算分子的最高次项
分子的最高次项为${(2x)}^{10}{(7x)}^{20} = {2}^{10}{x}^{10}{7}^{20}{x}^{20} = {2}^{10}{7}^{20}{x}^{30}$。
步骤 3：计算极限
分母为$5{x}^{30}$。当$x$趋向于无穷大时，只考虑分子分母的最高次项。因此，原式可化为$\lim _{x\rightarrow \infty }\dfrac {{2}^{10}{7}^{20}{x}^{30}}{5{x}^{30}}$。由于${x}^{30}$在分子和分母中相互抵消，极限值为$\dfrac {{2}^{10}{7}^{20}}{5}$。