题目
设函数f(x)满足lim _(harrow 0)dfrac (1)(h)[ f(5-dfrac (1)(3)h)-f(5)] =2,则lim _(harrow 0)dfrac (1)(h)[ f(5-dfrac (1)(3)h)-f(5)] =2 ____________.
设函数f(x)满足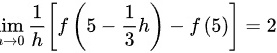 ,则
,则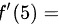 ____________.
____________.
题目解答
答案
本题考查的是导数的概念和定义,以及如何根据导数的定义来求解函数在某一点的导数值。
首先,我们需要理解导数的定义。导数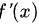 在点
在点
 的定义是:
的定义是: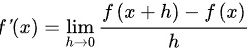
其次,根据题目给出的条件,我们有: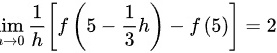
接下来,我们需要将上述极限表达式转换为导数的定义形式。注意到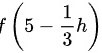 可以看作是
可以看作是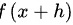 ,其中
,其中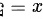 ,
,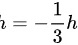 。因此,我们可以将极限表达式重写为:
。因此,我们可以将极限表达式重写为: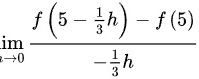
然后,我们需要将分子和分母同时乘以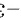 ,以消除分母中的负号和分数,得到:
,以消除分母中的负号和分数,得到: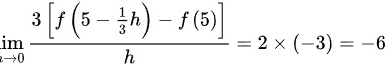 最后,根据导数的定义,我们可以得出
最后,根据导数的定义,我们可以得出
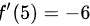 。
。
解析
步骤 1:理解导数的定义
导数$f'(x)$在点$x$的定义是:$f'(x)=\lim _{h\rightarrow 0}\dfrac {f(x+h)-f(x)}{h}$
步骤 2:将题目条件转换为导数定义形式
题目给出的条件是:$\lim _{h\rightarrow 0}\dfrac {1}{h}[ f(5-\dfrac {1}{3}h)-f(5)] =2$
注意到$f(5-\dfrac {1}{3}h)$可以看作是$f(x+h)$,其中$x=5$,$h=-\dfrac {1}{3}h$。因此,我们可以将极限表达式重写为:$\lim _{h\rightarrow 0}\dfrac {f(5-\dfrac {1}{3}h)-f(5)}{-\dfrac {1}{3}h}$
步骤 3:调整表达式以匹配导数定义
为了匹配导数的定义形式,我们需要将分子和分母同时乘以-3,以消除分母中的负号和分数,得到:$\lim _{h\rightarrow 0}\dfrac {3[ f(5-\dfrac {1}{3}h)-f(5)] }{h}=2\times (-3)=-6$
步骤 4:得出导数值
根据导数的定义,我们可以得出$f'(5)=-6$。
导数$f'(x)$在点$x$的定义是:$f'(x)=\lim _{h\rightarrow 0}\dfrac {f(x+h)-f(x)}{h}$
步骤 2:将题目条件转换为导数定义形式
题目给出的条件是:$\lim _{h\rightarrow 0}\dfrac {1}{h}[ f(5-\dfrac {1}{3}h)-f(5)] =2$
注意到$f(5-\dfrac {1}{3}h)$可以看作是$f(x+h)$,其中$x=5$,$h=-\dfrac {1}{3}h$。因此,我们可以将极限表达式重写为:$\lim _{h\rightarrow 0}\dfrac {f(5-\dfrac {1}{3}h)-f(5)}{-\dfrac {1}{3}h}$
步骤 3:调整表达式以匹配导数定义
为了匹配导数的定义形式,我们需要将分子和分母同时乘以-3,以消除分母中的负号和分数,得到:$\lim _{h\rightarrow 0}\dfrac {3[ f(5-\dfrac {1}{3}h)-f(5)] }{h}=2\times (-3)=-6$
步骤 4:得出导数值
根据导数的定义,我们可以得出$f'(5)=-6$。