题目
求下列不定积分:int dfrac (x+1)({x)^2+2x+5}dx;
求下列不定积分:
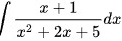 ;
;
题目解答
答案
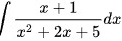
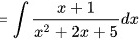
由第一类换元法可得
原式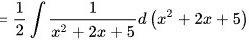
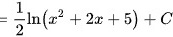
解析
步骤 1:分解被积函数
将被积函数 $\dfrac {x+1}{{x}^{2}+2x+5}$ 分解为两部分,以便于使用换元法。
步骤 2:使用换元法
令 $u = x^2 + 2x + 5$,则 $du = (2x + 2)dx = 2(x + 1)dx$,从而 $\dfrac{1}{2}du = (x + 1)dx$。
步骤 3:计算积分
将原积分转换为关于 $u$ 的积分,计算积分后,再将 $u$ 替换回 $x$ 的表达式。
将被积函数 $\dfrac {x+1}{{x}^{2}+2x+5}$ 分解为两部分,以便于使用换元法。
步骤 2:使用换元法
令 $u = x^2 + 2x + 5$,则 $du = (2x + 2)dx = 2(x + 1)dx$,从而 $\dfrac{1}{2}du = (x + 1)dx$。
步骤 3:计算积分
将原积分转换为关于 $u$ 的积分,计算积分后,再将 $u$ 替换回 $x$ 的表达式。