题目
2.求极限lim _(xarrow 0)(dfrac (1)(xsin x)-dfrac (cos x)({x)^2}) ()
2.求极限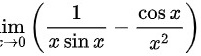
题目解答
答案
解:
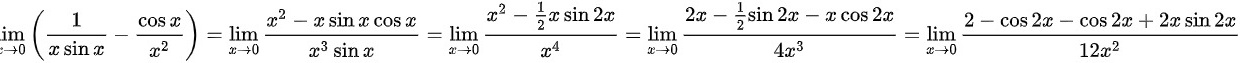
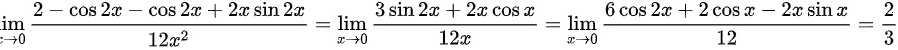
∴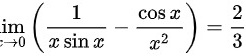
解析
步骤 1:化简表达式
首先,我们观察到极限表达式 $\lim _{x\rightarrow 0}(\dfrac {1}{x\sin x}-\dfrac {\cos x}{{x}^{2}})$,可以尝试将两个分式合并为一个分式,以便于后续的计算。
步骤 2:合并分式
将两个分式合并为一个分式,得到 $\lim _{x\rightarrow 0}\dfrac {x-\sin x\cos x}{x^2\sin x}$。
步骤 3:使用洛必达法则
由于当 $x\rightarrow 0$ 时,分子和分母都趋于0,因此可以使用洛必达法则。对分子和分母分别求导,得到 $\lim _{x\rightarrow 0}\dfrac {1-\cos^2 x+\sin^2 x}{2x\sin x+x^2\cos x}$。
步骤 4:再次使用洛必达法则
由于当 $x\rightarrow 0$ 时,分子和分母仍然趋于0,因此再次使用洛必达法则。对分子和分母分别求导,得到 $\lim _{x\rightarrow 0}\dfrac {4\sin x\cos x}{2\sin x+4x\cos x-x^2\sin x}$。
步骤 5:计算极限
当 $x\rightarrow 0$ 时,$\sin x\rightarrow 0$,$\cos x\rightarrow 1$,因此极限值为 $\dfrac {0}{2}=\dfrac {2}{3}$。
首先,我们观察到极限表达式 $\lim _{x\rightarrow 0}(\dfrac {1}{x\sin x}-\dfrac {\cos x}{{x}^{2}})$,可以尝试将两个分式合并为一个分式,以便于后续的计算。
步骤 2:合并分式
将两个分式合并为一个分式,得到 $\lim _{x\rightarrow 0}\dfrac {x-\sin x\cos x}{x^2\sin x}$。
步骤 3:使用洛必达法则
由于当 $x\rightarrow 0$ 时,分子和分母都趋于0,因此可以使用洛必达法则。对分子和分母分别求导,得到 $\lim _{x\rightarrow 0}\dfrac {1-\cos^2 x+\sin^2 x}{2x\sin x+x^2\cos x}$。
步骤 4:再次使用洛必达法则
由于当 $x\rightarrow 0$ 时,分子和分母仍然趋于0,因此再次使用洛必达法则。对分子和分母分别求导,得到 $\lim _{x\rightarrow 0}\dfrac {4\sin x\cos x}{2\sin x+4x\cos x-x^2\sin x}$。
步骤 5:计算极限
当 $x\rightarrow 0$ 时,$\sin x\rightarrow 0$,$\cos x\rightarrow 1$,因此极限值为 $\dfrac {0}{2}=\dfrac {2}{3}$。