题目
2.求下列函数在指定点的导数:-|||-(1) (x)=xsin x+dfrac (1)(2)cos x ,x=π/4;-|||-(2) (x)=dfrac (x-sin x)(x+sin x) =dfrac (pi )(2)
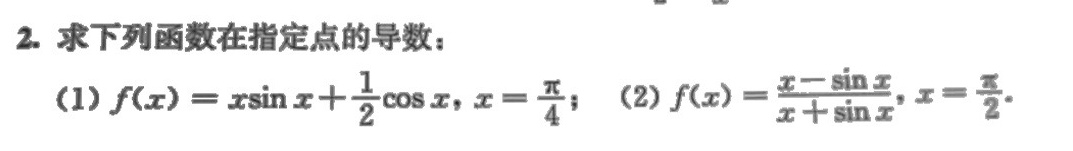
题目解答
答案

解析
步骤 1:求导数
对于函数 $f(x)=x\sin x+\dfrac {1}{2}\cos x$,我们首先需要求出它的导数。根据导数的求导法则,我们有:
$$f'(x) = \frac{d}{dx}(x\sin x) + \frac{d}{dx}(\frac{1}{2}\cos x)$$
$$f'(x) = \sin x + x\cos x - \frac{1}{2}\sin x$$
$$f'(x) = \frac{1}{2}\sin x + x\cos x$$
步骤 2:代入指定点
将 $x=\dfrac {\pi }{4}$ 代入导数 $f'(x)$ 中,得到:
$$f'(\frac{\pi}{4}) = \frac{1}{2}\sin \frac{\pi}{4} + \frac{\pi}{4}\cos \frac{\pi}{4}$$
$$f'(\frac{\pi}{4}) = \frac{1}{2}\cdot\frac{\sqrt{2}}{2} + \frac{\pi}{4}\cdot\frac{\sqrt{2}}{2}$$
$$f'(\frac{\pi}{4}) = \frac{\sqrt{2}}{4} + \frac{\sqrt{2}}{8}\pi$$
步骤 3:求导数
对于函数 $f(x)=\dfrac {x-\sin x}{x+\sin x}$,我们首先需要求出它的导数。根据导数的求导法则,我们有:
$$f'(x) = \frac{(x+\sin x)\frac{d}{dx}(x-\sin x) - (x-\sin x)\frac{d}{dx}(x+\sin x)}{(x+\sin x)^2}$$
$$f'(x) = \frac{(x+\sin x)(1-\cos x) - (x-\sin x)(1+\cos x)}{(x+\sin x)^2}$$
$$f'(x) = \frac{x - x\cos x + \sin x - \sin x\cos x - x - x\cos x + \sin x + \sin x\cos x}{(x+\sin x)^2}$$
$$f'(x) = \frac{-2x\cos x + 2\sin x}{(x+\sin x)^2}$$
步骤 4:代入指定点
将 $x=\dfrac {\pi }{2}$ 代入导数 $f'(x)$ 中,得到:
$$f'(\frac{\pi}{2}) = \frac{-2\cdot\frac{\pi}{2}\cos \frac{\pi}{2} + 2\sin \frac{\pi}{2}}{(\frac{\pi}{2}+\sin \frac{\pi}{2})^2}$$
$$f'(\frac{\pi}{2}) = \frac{2}{(\frac{\pi}{2}+1)^2}$$
$$f'(\frac{\pi}{2}) = \frac{8}{(\pi+2)^2}$$
对于函数 $f(x)=x\sin x+\dfrac {1}{2}\cos x$,我们首先需要求出它的导数。根据导数的求导法则,我们有:
$$f'(x) = \frac{d}{dx}(x\sin x) + \frac{d}{dx}(\frac{1}{2}\cos x)$$
$$f'(x) = \sin x + x\cos x - \frac{1}{2}\sin x$$
$$f'(x) = \frac{1}{2}\sin x + x\cos x$$
步骤 2:代入指定点
将 $x=\dfrac {\pi }{4}$ 代入导数 $f'(x)$ 中,得到:
$$f'(\frac{\pi}{4}) = \frac{1}{2}\sin \frac{\pi}{4} + \frac{\pi}{4}\cos \frac{\pi}{4}$$
$$f'(\frac{\pi}{4}) = \frac{1}{2}\cdot\frac{\sqrt{2}}{2} + \frac{\pi}{4}\cdot\frac{\sqrt{2}}{2}$$
$$f'(\frac{\pi}{4}) = \frac{\sqrt{2}}{4} + \frac{\sqrt{2}}{8}\pi$$
步骤 3:求导数
对于函数 $f(x)=\dfrac {x-\sin x}{x+\sin x}$,我们首先需要求出它的导数。根据导数的求导法则,我们有:
$$f'(x) = \frac{(x+\sin x)\frac{d}{dx}(x-\sin x) - (x-\sin x)\frac{d}{dx}(x+\sin x)}{(x+\sin x)^2}$$
$$f'(x) = \frac{(x+\sin x)(1-\cos x) - (x-\sin x)(1+\cos x)}{(x+\sin x)^2}$$
$$f'(x) = \frac{x - x\cos x + \sin x - \sin x\cos x - x - x\cos x + \sin x + \sin x\cos x}{(x+\sin x)^2}$$
$$f'(x) = \frac{-2x\cos x + 2\sin x}{(x+\sin x)^2}$$
步骤 4:代入指定点
将 $x=\dfrac {\pi }{2}$ 代入导数 $f'(x)$ 中,得到:
$$f'(\frac{\pi}{2}) = \frac{-2\cdot\frac{\pi}{2}\cos \frac{\pi}{2} + 2\sin \frac{\pi}{2}}{(\frac{\pi}{2}+\sin \frac{\pi}{2})^2}$$
$$f'(\frac{\pi}{2}) = \frac{2}{(\frac{\pi}{2}+1)^2}$$
$$f'(\frac{\pi}{2}) = \frac{8}{(\pi+2)^2}$$