题目
int dfrac (ln tan x)(cos xsin x)dx
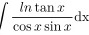
题目解答
答案
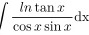
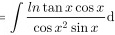

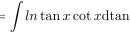

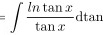

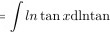

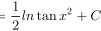
解析
步骤 1:转换积分变量
原积分式为 $\int \frac{\ln \tan x}{\cos x \sin x} dx$。注意到 $\cos x \sin x = \frac{1}{2} \sin 2x$,但更直接的转换是利用 $\tan x$ 的导数。令 $u = \tan x$,则 $du = \sec^2 x dx = \frac{1}{\cos^2 x} dx$。因此,$\frac{1}{\cos x \sin x} dx = \frac{1}{\sin x} \cdot \frac{1}{\cos x} dx = \frac{1}{\sin x} du$。由于 $\sin x = \frac{1}{\sqrt{1 + \tan^2 x}} = \frac{1}{\sqrt{1 + u^2}}$,则 $\frac{1}{\sin x} du = \sqrt{1 + u^2} du$。但更直接的是,注意到 $\frac{1}{\cos x \sin x} dx = \frac{1}{\tan x} d(\tan x)$,因此原积分可以写为 $\int \frac{\ln \tan x}{\tan x} d(\tan x)$。
步骤 2:积分计算
将 $u = \tan x$ 代入,原积分变为 $\int \frac{\ln u}{u} du$。这是一个标准的积分形式,可以通过分部积分法解决。设 $v = \ln u$,$dw = \frac{1}{u} du$,则 $dv = \frac{1}{u} du$,$w = \ln u$。根据分部积分公式 $\int v dw = vw - \int w dv$,我们得到 $\int \frac{\ln u}{u} du = \frac{1}{2} \ln^2 u + C$。
步骤 3:回代变量
将 $u = \tan x$ 回代,得到最终结果。
原积分式为 $\int \frac{\ln \tan x}{\cos x \sin x} dx$。注意到 $\cos x \sin x = \frac{1}{2} \sin 2x$,但更直接的转换是利用 $\tan x$ 的导数。令 $u = \tan x$,则 $du = \sec^2 x dx = \frac{1}{\cos^2 x} dx$。因此,$\frac{1}{\cos x \sin x} dx = \frac{1}{\sin x} \cdot \frac{1}{\cos x} dx = \frac{1}{\sin x} du$。由于 $\sin x = \frac{1}{\sqrt{1 + \tan^2 x}} = \frac{1}{\sqrt{1 + u^2}}$,则 $\frac{1}{\sin x} du = \sqrt{1 + u^2} du$。但更直接的是,注意到 $\frac{1}{\cos x \sin x} dx = \frac{1}{\tan x} d(\tan x)$,因此原积分可以写为 $\int \frac{\ln \tan x}{\tan x} d(\tan x)$。
步骤 2:积分计算
将 $u = \tan x$ 代入,原积分变为 $\int \frac{\ln u}{u} du$。这是一个标准的积分形式,可以通过分部积分法解决。设 $v = \ln u$,$dw = \frac{1}{u} du$,则 $dv = \frac{1}{u} du$,$w = \ln u$。根据分部积分公式 $\int v dw = vw - \int w dv$,我们得到 $\int \frac{\ln u}{u} du = \frac{1}{2} \ln^2 u + C$。
步骤 3:回代变量
将 $u = \tan x$ 回代,得到最终结果。