题目
设(x)=dfrac (1-x)(1+x), 则(x)=dfrac (1-x)(1+x)
设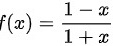 , 则
, 则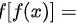
题目解答
答案
令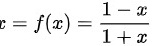 ,代入所以有
,代入所以有
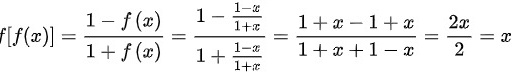
综上可得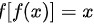
解析
步骤 1:定义函数$f(x)$
给定函数$f(x)=\dfrac {1-x}{1+x}$,我们需要计算$f[f(x)]$的值。
步骤 2:计算$f[f(x)]$
首先,我们令$z=f(x)=\dfrac {1-x}{1+x}$,然后将$z$代入$f(x)$中,得到$f[f(x)]$的表达式。
$f[f(x)] = f(z) = \dfrac {1-z}{1+z}$
步骤 3:代入$z$的值
将$z=\dfrac {1-x}{1+x}$代入$f(z)$中,得到$f[f(x)]$的表达式。
$f[f(x)] = \dfrac {1-\dfrac {1-x}{1+x}}{1+\dfrac {1-x}{1+x}}$
步骤 4:化简表达式
化简$f[f(x)]$的表达式,得到最终结果。
$f[f(x)] = \dfrac {1-\dfrac {1-x}{1+x}}{1+\dfrac {1-x}{1+x}} = \dfrac {\dfrac {1+x-(1-x)}{1+x}}{\dfrac {1+x+(1-x)}{1+x}} = \dfrac {\dfrac {2x}{1+x}}{\dfrac {2}{1+x}} = \dfrac {2x}{2} = x$
给定函数$f(x)=\dfrac {1-x}{1+x}$,我们需要计算$f[f(x)]$的值。
步骤 2:计算$f[f(x)]$
首先,我们令$z=f(x)=\dfrac {1-x}{1+x}$,然后将$z$代入$f(x)$中,得到$f[f(x)]$的表达式。
$f[f(x)] = f(z) = \dfrac {1-z}{1+z}$
步骤 3:代入$z$的值
将$z=\dfrac {1-x}{1+x}$代入$f(z)$中,得到$f[f(x)]$的表达式。
$f[f(x)] = \dfrac {1-\dfrac {1-x}{1+x}}{1+\dfrac {1-x}{1+x}}$
步骤 4:化简表达式
化简$f[f(x)]$的表达式,得到最终结果。
$f[f(x)] = \dfrac {1-\dfrac {1-x}{1+x}}{1+\dfrac {1-x}{1+x}} = \dfrac {\dfrac {1+x-(1-x)}{1+x}}{\dfrac {1+x+(1-x)}{1+x}} = \dfrac {\dfrac {2x}{1+x}}{\dfrac {2}{1+x}} = \dfrac {2x}{2} = x$