题目
21.设二次型((x)_(1),(x)_(2),(x)_(3))=(a)_(1)({x)_(1)}^2+(a)_({x)_(2)}^2+(a-1)({x)_(3)}^2+2(x)_(1)(x)_(1)(a为常数)。(1)求一个正交变换((x)_(1),(x)_(2),(x)_(3))=(a)_(1)({x)_(1)}^2+(a)_({x)_(2)}^2+(a-1)({x)_(3)}^2+2(x)_(1)(x)_(1)将((x)_(1),(x)_(2),(x)_(3))=(a)_(1)({x)_(1)}^2+(a)_({x)_(2)}^2+(a-1)({x)_(3)}^2+2(x)_(1)(x)_(1)化为标准形;(2)设((x)_(1),(x)_(2),(x)_(3))=(a)_(1)({x)_(1)}^2+(a)_({x)_(2)}^2+(a-1)({x)_(3)}^2+2(x)_(1)(x)_(1),求方程((x)_(1),(x)_(2),(x)_(3))=(a)_(1)({x)_(1)}^2+(a)_({x)_(2)}^2+(a-1)({x)_(3)}^2+2(x)_(1)(x)_(1)的全部解。
21.
设二次型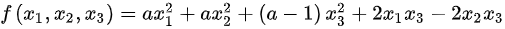 (a为常数)。
(a为常数)。
(1)求一个正交变换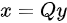 将
将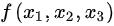 化为标准形;
化为标准形;
(2)设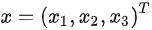 ,求方程
,求方程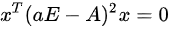 的全部解。
的全部解。
题目解答
答案
(1)已知二次型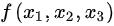 ,可写出矩阵
,可写出矩阵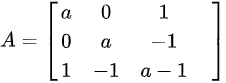 ,则
,则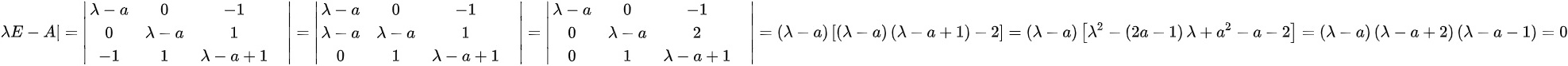 ;故矩阵A的特征值为
;故矩阵A的特征值为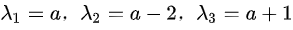 ;
;
解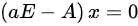 ,有
,有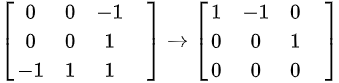 ,得到特征向量
,得到特征向量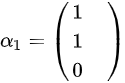 ;
;
解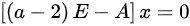 ,有
,有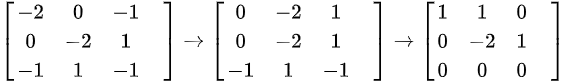 ,得到特征向量
,得到特征向量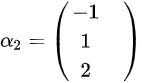 ;
;
解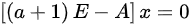 ,有
,有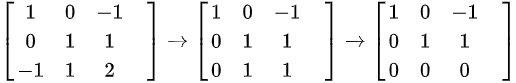 ,得到特征向量
,得到特征向量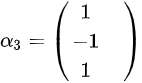 。因为这三个特征向量两两正交,故有
。因为这三个特征向量两两正交,故有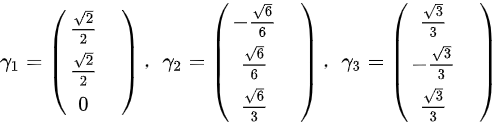 ,故
,故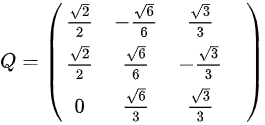 ,
,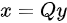 ,使得二次型化为规范形
,使得二次型化为规范形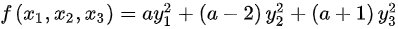
(2)算出矩阵B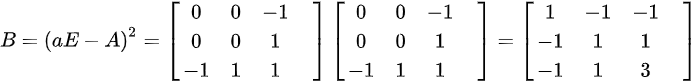 ,
,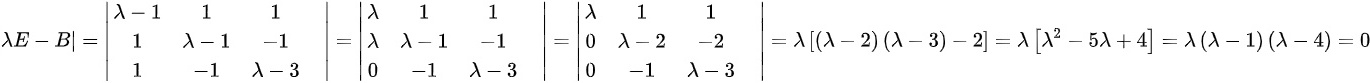 ,故矩阵B的特征值为
,故矩阵B的特征值为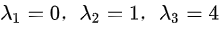 .
.
解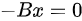 ,有
,有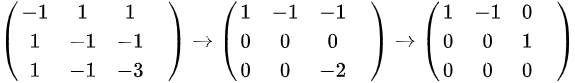 ,得到特征向量
,得到特征向量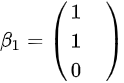 ;
;
解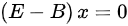 ,有
,有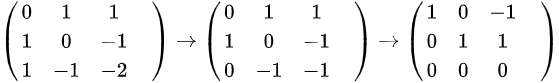 ,得到特征向量
,得到特征向量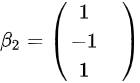 ;
;
解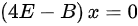 ,有
,有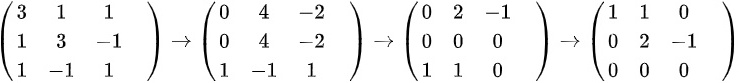 ,得到特征向量
,得到特征向量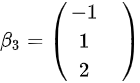 。因为这三个特征向量两两相交,则有
。因为这三个特征向量两两相交,则有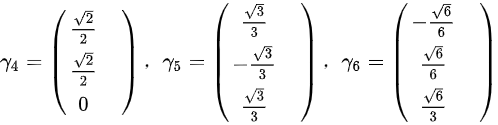 ;
;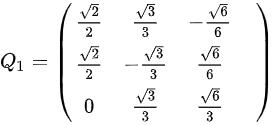 ,故当
,故当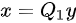 时,
时,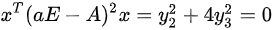 ,有
,有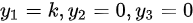 (k为任意常数)。最终可求得该解:
(k为任意常数)。最终可求得该解:
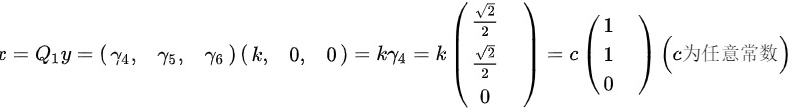 。即
。即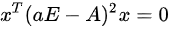 的解为
的解为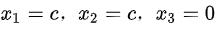 。
。