题目
int dfrac (tan x)(sqrt {cos x)}dx=_____.
_____.
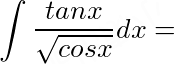题目解答
答案
.
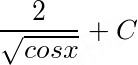解析
步骤 1：代换
设 $u = \cos x$，则 $du = -\sin x dx$，即 $dx = -\frac{1}{\sin x} du$。同时，$\tan x = \frac{\sin x}{\cos x} = \frac{\sin x}{u}$。
步骤 2：代入
将 $u$ 和 $dx$ 的表达式代入原积分，得到 $\int \frac{\tan x}{\sqrt{\cos x}} dx = \int \frac{\frac{\sin x}{u}}{\sqrt{u}} \left(-\frac{1}{\sin x}\right) du = -\int \frac{1}{u\sqrt{u}} du$。
步骤 3：积分
$-\int \frac{1}{u\sqrt{u}} du = -\int u^{-\frac{3}{2}} du = -\frac{u^{-\frac{1}{2}}}{-\frac{1}{2}} + C = 2u^{-\frac{1}{2}} + C = \frac{2}{\sqrt{u}} + C$。
步骤 4：回代
将 $u = \cos x$ 回代，得到 $\frac{2}{\sqrt{\cos x}} + C$。
设 $u = \cos x$，则 $du = -\sin x dx$，即 $dx = -\frac{1}{\sin x} du$。同时，$\tan x = \frac{\sin x}{\cos x} = \frac{\sin x}{u}$。
步骤 2：代入
将 $u$ 和 $dx$ 的表达式代入原积分，得到 $\int \frac{\tan x}{\sqrt{\cos x}} dx = \int \frac{\frac{\sin x}{u}}{\sqrt{u}} \left(-\frac{1}{\sin x}\right) du = -\int \frac{1}{u\sqrt{u}} du$。
步骤 3：积分
$-\int \frac{1}{u\sqrt{u}} du = -\int u^{-\frac{3}{2}} du = -\frac{u^{-\frac{1}{2}}}{-\frac{1}{2}} + C = 2u^{-\frac{1}{2}} + C = \frac{2}{\sqrt{u}} + C$。
步骤 4：回代
将 $u = \cos x$ 回代，得到 $\frac{2}{\sqrt{\cos x}} + C$。