题目
求极限：lim _(xarrow infty )((dfrac {{x)^2+2}({x)^2+2x+1})}^x
求极限：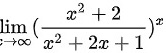
题目解答
答案
求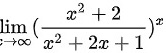，首先可对其进行变形：
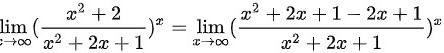
(注：目的是凑重要极限式：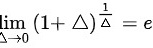
中底数的形式)
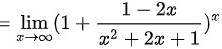
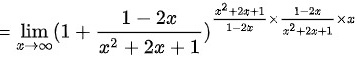
（注：凑重要极限中幂的形式）
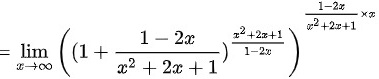
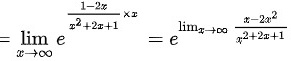（注：使用了总要极限）
而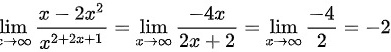
（注：此极限使用了洛必达法则，当x趋近于无穷时，该极限式为无穷比无穷型，可使用洛必达法则求极限）
故：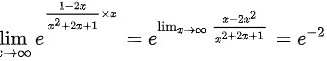
即：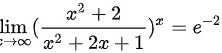
解析
步骤 1：变形
首先，我们对给定的极限式进行变形，以便于使用重要极限式 $\lim _{\Delta \rightarrow 0}{(1+\Delta )}^{\dfrac {1}{\Delta }}=e$。我们有：
$$\lim _{x\rightarrow \infty }{(\dfrac {{x}^{2}+2}{{x}^{2}+2x+1})}^{x}=\lim _{x\rightarrow \infty }{(\dfrac {{x}^{2}+2x+1-2x+1}{{x}^{2}+2x+1})}^{x}$$
步骤 2：凑重要极限式
接下来，我们凑重要极限式的形式，即底数的形式：
$$\lim _{x\rightarrow \infty }{(1+\dfrac {1-2x}{{x}^{2}+2x+1})}^{x}$$
步骤 3：凑幂的形式
然后，我们凑幂的形式，以便于使用重要极限式：
$$\lim _{x\rightarrow \infty }{(1+\dfrac {1-2x}{{x}^{2}+2x+1})}^{\dfrac {{x}^{2}+2x+1}{1-2x}\times \dfrac {1-2x}{{x}^{2}+2x+1}\times x}$$
步骤 4：计算幂的极限
计算幂的极限，使用洛必达法则：
$$\lim _{x\rightarrow \infty }\dfrac {x-2{x}^{2}}{{x}^{2}+2x+1}=\lim _{x\rightarrow \infty }\dfrac {-4x}{2x+2}=\lim _{x\rightarrow \infty }\dfrac {-4}{2}=-2$$
步骤 5：计算最终极限
最后，我们计算最终的极限：
$$\lim _{x\rightarrow \infty }{(\dfrac {{x}^{2}+2}{{x}^{2}+2x+1})}^{x}={e}^{-2}$$
首先，我们对给定的极限式进行变形，以便于使用重要极限式 $\lim _{\Delta \rightarrow 0}{(1+\Delta )}^{\dfrac {1}{\Delta }}=e$。我们有：
$$\lim _{x\rightarrow \infty }{(\dfrac {{x}^{2}+2}{{x}^{2}+2x+1})}^{x}=\lim _{x\rightarrow \infty }{(\dfrac {{x}^{2}+2x+1-2x+1}{{x}^{2}+2x+1})}^{x}$$
步骤 2：凑重要极限式
接下来，我们凑重要极限式的形式，即底数的形式：
$$\lim _{x\rightarrow \infty }{(1+\dfrac {1-2x}{{x}^{2}+2x+1})}^{x}$$
步骤 3：凑幂的形式
然后，我们凑幂的形式，以便于使用重要极限式：
$$\lim _{x\rightarrow \infty }{(1+\dfrac {1-2x}{{x}^{2}+2x+1})}^{\dfrac {{x}^{2}+2x+1}{1-2x}\times \dfrac {1-2x}{{x}^{2}+2x+1}\times x}$$
步骤 4：计算幂的极限
计算幂的极限，使用洛必达法则：
$$\lim _{x\rightarrow \infty }\dfrac {x-2{x}^{2}}{{x}^{2}+2x+1}=\lim _{x\rightarrow \infty }\dfrac {-4x}{2x+2}=\lim _{x\rightarrow \infty }\dfrac {-4}{2}=-2$$
步骤 5：计算最终极限
最后，我们计算最终的极限：
$$\lim _{x\rightarrow \infty }{(\dfrac {{x}^{2}+2}{{x}^{2}+2x+1})}^{x}={e}^{-2}$$