题目
下列等式成立的是（ ）。A.|f(x)dx=f(x)+CB.|f(x)dx=f(x)+CC.|f(x)dx=f(x)+CD.|f(x)dx=f(x)+C
下列等式成立的是（ ）。
A.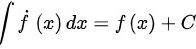
B.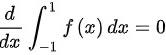
C.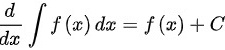
D.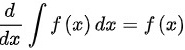
题目解答
答案
先求导后求积分，则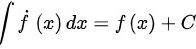；先求定积分得到一个常数再求导（常数的导数为0），则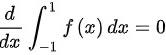；先求积分再求导，则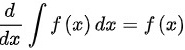。选ABD。
解析
步骤 1：分析选项A
选项A表示的是不定积分的定义，即求函数$f(x)$的原函数，加上任意常数$C$。因此，$\int f(x)dx=f(x)+C$是正确的。
步骤 2：分析选项B
选项B表示的是对定积分求导。定积分${\int }_{-1}^{1}f(x)dx$是一个常数，因为积分限是固定的。常数的导数为0，因此$\dfrac {d}{dx}{\int }_{-1}^{1}f(x)dx=0$是正确的。
步骤 3：分析选项C
选项C的表达式不正确，因为积分符号后面应该是一个函数，而不是$f(x)dx$。因此，$\dfrac {d}{dx}{\int }_{f(x)dx}=f(x)+C$是错误的。
步骤 4：分析选项D
选项D表示的是对不定积分求导。根据微积分基本定理，不定积分的导数就是被积函数本身，因此$\dfrac {d}{dx}{\int }_{f}(x)dx=f(x)$是正确的。
选项A表示的是不定积分的定义，即求函数$f(x)$的原函数，加上任意常数$C$。因此，$\int f(x)dx=f(x)+C$是正确的。
步骤 2：分析选项B
选项B表示的是对定积分求导。定积分${\int }_{-1}^{1}f(x)dx$是一个常数，因为积分限是固定的。常数的导数为0，因此$\dfrac {d}{dx}{\int }_{-1}^{1}f(x)dx=0$是正确的。
步骤 3：分析选项C
选项C的表达式不正确，因为积分符号后面应该是一个函数，而不是$f(x)dx$。因此，$\dfrac {d}{dx}{\int }_{f(x)dx}=f(x)+C$是错误的。
步骤 4：分析选项D
选项D表示的是对不定积分求导。根据微积分基本定理，不定积分的导数就是被积函数本身，因此$\dfrac {d}{dx}{\int }_{f}(x)dx=f(x)$是正确的。