题目
设函数 y=y(x) 由方程 -x(e)^y=1 所确定,求 dfrac ({d)^2y}(d{x)^2}(|)_(x=0) 的值.
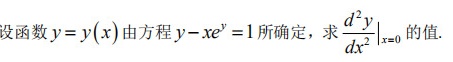
题目解答
答案
解析:
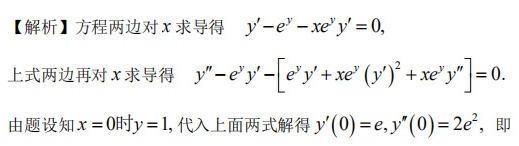
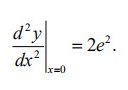
解析
步骤 1:对给定方程进行隐函数求导
给定方程为 $y-x{e}^{y}=1$。首先,对x求导,得到 $y'-{e}^{y}-x{e}^{y}y'=0$。
步骤 2:求解一阶导数 $y'(x)$
从步骤1得到的方程中解出 $y'$,得到 $y'=\frac{{e}^{y}}{1-x{e}^{y}}$。
步骤 3:求解二阶导数 $y''(x)$
对步骤2得到的 $y'$ 再次对x求导,得到 $y''=\frac{{e}^{y}(1-x{e}^{y})-{e}^{y}(-{e}^{y}-x{e}^{y}y')}{(1-x{e}^{y})^{2}}$。
步骤 4:代入 $x=0$ 和 $y=1$ 求解 $y''(0)$
由原方程 $y-x{e}^{y}=1$,当 $x=0$ 时,$y=1$。将 $x=0$ 和 $y=1$ 代入步骤3得到的 $y''$ 表达式中,得到 $y''(0)=2{e}^{2}$。
给定方程为 $y-x{e}^{y}=1$。首先,对x求导,得到 $y'-{e}^{y}-x{e}^{y}y'=0$。
步骤 2:求解一阶导数 $y'(x)$
从步骤1得到的方程中解出 $y'$,得到 $y'=\frac{{e}^{y}}{1-x{e}^{y}}$。
步骤 3:求解二阶导数 $y''(x)$
对步骤2得到的 $y'$ 再次对x求导,得到 $y''=\frac{{e}^{y}(1-x{e}^{y})-{e}^{y}(-{e}^{y}-x{e}^{y}y')}{(1-x{e}^{y})^{2}}$。
步骤 4:代入 $x=0$ 和 $y=1$ 求解 $y''(0)$
由原方程 $y-x{e}^{y}=1$,当 $x=0$ 时,$y=1$。将 $x=0$ 和 $y=1$ 代入步骤3得到的 $y''$ 表达式中,得到 $y''(0)=2{e}^{2}$。