题目
求下列极限lim _(xarrow 0)dfrac (tan x-x)(x-sin x)。
求下列极限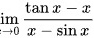
。
题目解答
答案
由题可知，所给的已知条件为函数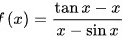
，以及题目所求为极限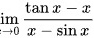，由此可知本题需要利用常用等价无穷小公式的基本性质和运算法则来对本题目进行分析计算。
当自变量无限趋近于无穷小量即
时，有常用等价无穷小公式分别为：
；
。
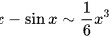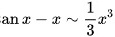因此，极限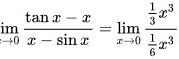
。
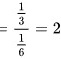综上所述，极限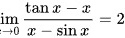
.
解析
步骤 1：确定等价无穷小
当$x\rightarrow 0$时，有常用等价无穷小公式：
$\tan x-x\sim \dfrac {1}{3}{x}^{3}$；
$x-\sin x\sim \dfrac {1}{6}{x}^{3}$。
步骤 2：代入等价无穷小
将上述等价无穷小代入原极限中，得到：
$\lim _{x\rightarrow 0}\dfrac {\tan x-x}{x-\sin x}=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{\dfrac {1}{6}{x}^{3}}$。
步骤 3：计算极限
计算上述极限，得到：
$\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{\dfrac {1}{6}{x}^{3}}=\dfrac {\dfrac {1}{3}}{\dfrac {1}{6}}=2$。
当$x\rightarrow 0$时，有常用等价无穷小公式：
$\tan x-x\sim \dfrac {1}{3}{x}^{3}$；
$x-\sin x\sim \dfrac {1}{6}{x}^{3}$。
步骤 2：代入等价无穷小
将上述等价无穷小代入原极限中，得到：
$\lim _{x\rightarrow 0}\dfrac {\tan x-x}{x-\sin x}=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{\dfrac {1}{6}{x}^{3}}$。
步骤 3：计算极限
计算上述极限，得到：
$\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{\dfrac {1}{6}{x}^{3}}=\dfrac {\dfrac {1}{3}}{\dfrac {1}{6}}=2$。