题目
=dfrac (sqrt {64-{x)^2}}(ln (x-5)) 定义域
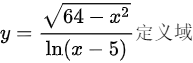
题目解答
答案
根据函数y的表达式，可以得到x应满足x-5≠1,且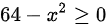
,因此综合两个不等式，可以得到x的取值范围是[-8,6)U(6,8].即函数y的定义域是[-8,6)U(6,8]。
解析
步骤 1：确定根号内的表达式非负
为了使根号内的表达式有意义，需要满足$64 - x^2 \geq 0$。解这个不等式，得到$x^2 \leq 64$，即$-8 \leq x \leq 8$。
步骤 2：确定对数函数的定义域
为了使对数函数有意义，需要满足$x - 5 > 0$，即$x > 5$。同时，对数函数的底数不能为1，因此$x - 5 \neq 1$，即$x \neq 6$。
步骤 3：综合两个条件
结合步骤1和步骤2的条件，可以得到$x$的取值范围是$5 < x \leq 8$且$x \neq 6$。因此，函数$y$的定义域是$(5, 6) \cup (6, 8]$。
为了使根号内的表达式有意义，需要满足$64 - x^2 \geq 0$。解这个不等式，得到$x^2 \leq 64$，即$-8 \leq x \leq 8$。
步骤 2：确定对数函数的定义域
为了使对数函数有意义，需要满足$x - 5 > 0$，即$x > 5$。同时，对数函数的底数不能为1，因此$x - 5 \neq 1$，即$x \neq 6$。
步骤 3：综合两个条件
结合步骤1和步骤2的条件，可以得到$x$的取值范围是$5 < x \leq 8$且$x \neq 6$。因此，函数$y$的定义域是$(5, 6) \cup (6, 8]$。